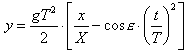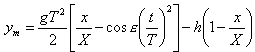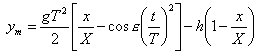Il tiro con grande angolo di sito

Talvolta, e particolarmente nella caccia di montagna, occorre sparare a bersagli che non si trovano sullo stesso orizzonte del cacciatore, ma molto più a monte od a valle. L'arma dovrà assumere quindi una notevole inclinazione verso l'alto o verso il basso: in tali condizioni non può più farsi affidamento sulla teoria della rotazione della traiettoria, che anzi dà luogo ad errori tali da far bellamente mancare il bersaglio. In altre parole, non è possibile sparare ad un camoscio posto a 200 metri sopra di noi, su di una cengia, senza tener conto del diverso angolo di sito, poiché l'arma è azzerata per una traiettoria con angolo di sito modesto (in pratica si comincia a considerare rilevante l'errore oltre un angolo di sito di 30°.

Esaminando la figura

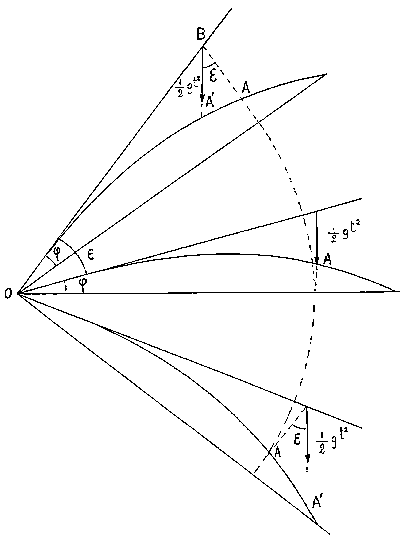
sarà subito chiara la causa del fenomeno.
Un proiettile sparato con l'angolo di proiezione j e angolo di sito nullo, giungerà dopo il tempo -t- nel punto A, ottenuto secondo i principi già esaminati, supponendo che il proiettile si muova prima lungo la linea di proiezione per effetto dell'impulso iniziale e cada poi perpendicolarmente per il tempo -t- per effetto della forza di gravità. Se ora si spara invece con l'angolo di sito e (è indifferente se positivo o negativo) il proiettile non cadrà per effetto della forza di gravità in A ma bensì in A'; la conseguenza sarà, che, alla medesima distanza di azzeramento, il proiettile seguirà una traiettoria più alta rispetto alla linea di sito (o di mira) e che quindi, per colpire il centro del bersaglio, occorrerà mirare più in basso.
La figura non è in scala e le dimensioni sono state volutamente esagerate per evidenziare meglio il fenomeno.
La traiettoria del proiettile sparato con angolo di sito diverso da zero può essere agevolmente tracciata con il sistema proposto da Francé Avcin. Egli, in primo luogo, semplifica il problema osservando che l'angolo j , di pochi secondi, può essere tranquillamente trascurato rispetto all'angolo e ; osserva inoltre che il tratto di traiettoria compreso tra A ed A' è anch'esso trascurabile rispetto all'intero arco dio 150-200 metri in quanto non supera i 15-20 cm di lunghezza. Infatti, come si vede nella figura, l'angolo formato dai tratti HA e HA' è eguale all'angolo e e perciò il tratto AA' sarà dato dalla formula AA' = (gt² . sen e )/2
Esempio: sia e =60° e t= 0,255 sec.

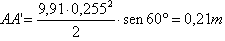
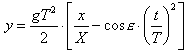
La traiettoria potrà perciò essere tranquillamente calcolata come se A' cadesse sul tratto BA usando la formula già vista per le traiettorie venatorie , opportunamente integrata. Ricordo che t = tempo di volo alle varie distanze x a cui si vuole calcolare la caduta; T = tempo di volo alla distanza a cui è azzerata l'arma; X = tempo di volo alla distanza di azzeramento. 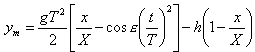Le ordinate progressive alle varie distanze, secondo la linea di sito, saranno date dalla formula E le ordinate progressive rispetto alla linea di mira, dalla formula

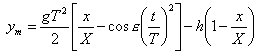
Vediamo, come al solito, un esempio concreto calcolato con riferimento alla cartuccia 6,5 x 57 VM della RWS con pallottola di 6 gr e V= 1010 ms e DOA = 200 m. Dalla tavola della casa, integrata con il metodo già visto si ottengono i seguenti tempi di volo

A metri   50    100    150    200    250    300    350     400
Tempo   0,051  0,105  0,163  0,255  0,340  0,368  0,453   0,540 
  

da cui si calcolano le seguenti ordinate progressive per il tiro in piano e per il tiro con angolo di sito di 60° riferite alla linea di mira

          y50    y100    y150   y200    y300    y350
e = 0°   0,011   0,045   0,043   *      - 0,26          metri
e = 60°          0,072          0,12    0,065   -0,03   metri

Con queste ordinate può quindi procedersi al tracciamento grafico delle relative traiettorie, sia per e positivo che negativo, come nella figura

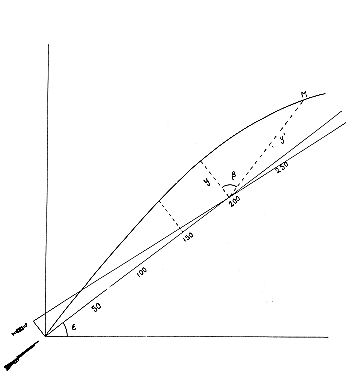
ove è stata usata la scala grafica già impiegata nel capitolo sulla traiettoria venatoria.
Dall' immagine si vede che il punto in bianco viene a cadere a circa 340 metri di distanza e che a 200 metri il proiettile colpisce ben 12 cm. al di sopra della linea di mira, il che può certamente far mancare il bersaglio o arrecare ferite non mortali. Il tiratore quindi, se da un lato deve preoccuparsi meno della valutazione della distanza a cui si trova il bersaglio, dal momento che il proiettile viaggia sempre al di sopra della linea di mira anche oltre la distanza di 300 metri, d'altro lato deve tener presente che il proiettile colpirà più in alto del punto mirato. Le indicazioni fornite consentono di tracciare agevolmente una serie di traiettorie per diversi angoli di sito (è sufficiente procedere di 15° in 15° più che sufficienti per l'uso del cacciatore).
Ciò posto occorre ora esaminare come il cacciatore od il tiratore debbano agire per correggere lo spostamento della traiettoria. Se il bersaglio si trovasse ad essere posto perpendicolarmente alla traiettoria percorsa dal proiettile (si pensi ad un uccello in volo), non vi sarebbero particolari difficoltà poichè sarebbe sufficiente mirare ad un punto posto al di sotto del bersaglio della misura y, per fare centro. In genere però (fig. 3b) il bersaglio si presenta al tiratore come verticale e quindi, per effetto dell'angolo di sito, viene visto sotto una prospettiva molto allungata ed interseca la traiettoria trasversalmente.

La conseguenza di ciò è che mirando al centro del bersaglio, il proiettile colpirà invece il punto M posto al di sopra del bersaglio della quantità y'. Bisognerà quindi mirare la punto M' simmetrico al precedente, ma in basso.
Questo valore di y' è ricavabile da y mediante la formula y' = y/cose

Esempio: L'ordinata progressiva prima calcolata per la distanza di 200 m. ed e = 60° è di cm.12; la formula precedente ci dice che y' = 24 cm.

Un piccolo programma per DOS vi aiuterà nel calcolo. Quando l'arma sia dotata di tacche di mira o di alzo che consentano l'azzeramento a distanze variabili, la correzione del tiro può essere ottenuta in maniera abbastanza soddisfacente azzerando l'arma ad una distanza minore di quella a cui è posto il bersaglio e precisamente alla distanza che si ottiene moltiplicando la distanza effettiva per il coseno dell'angolo di sito.
Esempio: Sia la traiettoria sopra calcolata con angolo di sito e = 60° e bersaglio a 200 metri, pari alla distanza ottimale di azzeramento. Se l'arma viene azzerata alla distanza

200 * cos e = 100 m
si otterrà una traiettoria che colpirà il bersaglio con errore trascurabile. Questa traiettoria però è molto tesa fino a 200 metri, ma poi si distacca negativamente dalla linea di sito così che un errore anche modesto, in difetto, nella valutazione della distanza del bersaglio, può causare un errore inaccettabile. Conviene perciò abituarsi a correggere la mira ad occhio.
Se l'angolo di sito fosse di 75° si dovrebbe azzerare a 50 metri per fare centro a 200 metri.