Balistica venatoria - La traiettoria utile

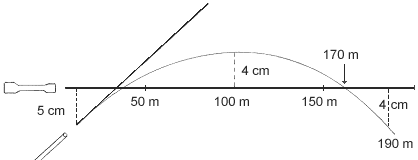
Figura I

La balistica esterna ha il compito di consentire il calcolo di gittate di ogni genere, sia per proiettili di piccolo calibro che di artiglierie.
Alla maggior parte delle persone accade però ben di rado di dover calcolare traiettorie di chilometri, ma hanno bisogno di conoscere i dati di tiro della propria arma nell'ambito della gittata di pratico impiego, vale a dire tre o quattrocento metri al massimo per i fucili a palla e un centinaio di metri al massimo per le armi corte.

I dati relativi a questo tipo di traiettoria possono essere calcolati con ottima precisione, partendo dai pochi dati forniti dal produttore delle munizioni o dai dati misurati con un cronografo. Il calcolo, relativo a traiettorie molto tese e con angolo di proiezione minimo, richiede una notevole precisione poiché non si può trascurare, come avviene per le lunghe gittate, la circostanza che la linea di proiezione non coincide con la linea di mira.
Come si vede dalla figura I, in cui la curvatura della traiettoria è stata volutamente esagerata per meglio rappresentare il fenomeno, la traiettoria interseca due volte la linea di mira; una prima volta ad una distanza di 20-40 metri dalla bocca dell'arma e una seconda volta alla distanza per la quale l'arma è stata azzerata.
Un primo punto di partenza per lo studio della traiettoria venatoria è dato dalle tabelle balistiche che le fabbriche di munizioni forniscono per le proprie cartucce e di cui quindi occorre apprendere l'uso ed il significato.
Le tavole europee hanno il contenuto di quella qui riportata per una cartuccia della RWS
Cartuccia RWS 7x64 HMK - DATI BALISTICI
Peso del proiettile 11,2 gr
Peso della polvere 3,75 gr
Lunghezza del proiettile 34 mm
Lunghezza della canna 650 mm
Pressione massima 3600 kg/cm²
Velocità a 10 m. 840 m/sec

Distanza Energia  Velocità   Tempo di
   m       Kgm      m/sec    volo sec
  0        412       850        0
  50       370       805      0,060
  100      334       765      0,123
  150      300       725      0,190
  200      272       690      0,260
  300      219       620      0,411

 DISTANZA DEL PUNTO DI IMPATTO DALLA LINEA DI MIRA IN CM

Dist   DOA a   Con cannocchiale e taratura a:  Senza cann.
 m     m 170    100m     150m    200m    300m     100m

50      +1,5    -0,5     +0,5    +2,5    +6,5      +1
100     +4        *      +2,5    +6      +14        *
150     +2      -4         *     +5      +17       -5,5
200     -4,5    -12      -7       *      +16       -15
300     -31     -42      -35     -24      *        -48
  

Il significato dei dati è presto detto; sono indicate le ordinate progressive di cinque traiettorie secondo cinque diverse distanze di azzeramento e con impiego di cannocchiale (convenzionalmente supposto avere l'asse ottico a 5 cm sopra l'asse della canna) e quelle di una traiettoria con impiego dei punti di mira meccanici, convenzionalmente supposti essere a due cm sopra l'asse della canna. È indicata inoltre la traiettoria per la distanza ottimale di azzeramento (DOA), con cannocchiale.
I dati ci dicono quindi che per un azzeramento ottimale a 170 metri, se il bersaglio è posto a 100 metri il proiettile colpirà 4 cm più in alto e che se il bersaglio è posto a 300 metri il proiettile colpirà 31 cm più in basso rispetto al punto mirato.
I valori delle ordinate sono riferiti, si ripete, a linee di mira convenzionali; quindi per avere dati veramente precisi, validi nel caso specifico, occorre misurare l'effettiva distanza tra asse del cannocchiale e asse della canna (ad esempio esso può essere superiore a 5 cm nei combinati); occorre poi tener conto delle variazioni di velocità del proiettile a seconda della lunghezza della canna e degli altri fattori già visti. Nella tabella è indicata molto opportunamente anche la velocità a 10 metri dalla volata perché la velocità iniziale viene calcolata teoricamente da essa.
Le tabelle dei paesi anglosassoni sono alquanto più sintetiche ed in genere, invece di indicare le ordinate progressive, si limitano ad indicare il valore della mid-range trajectory e cioè il valore dell'ordinata presa a metà della gittata e misurata rispetto alla linea di sito. Talvolta esse sono compilate secondo il modello europeo ma con i dati riferiti a 100, 200, 300 yarde e secondo una linea di mira per cannocchiale pari a un pollice e mezzo (3,8 cm) sopra l'asse della canna.

Un concetto da chiarire è quello delle distanza ottimale di azzeramento (DOA): questa indica quella gittata alla quale la traiettoria percorsa dal proiettile non supera mai la distanza (positiva o negativa, di 4 cm dalla linea di mira; in altre parole ciò significa che se la DOA di un proiettile è di 170 metri, qualunque bersaglio posto tra la bocca dell'arma e tale distanza (alla quale debbono aggiungersi 20-30 metri in cui il proiettile scende al di sotto della linea di mira per un valore inferiore e 4 cm, verrà colpito con uno scarto massimo di 4 cm riferito alla linea di mira. Questo ovviamente in linea teorica se non intervengono cause di dispersione del tiro. È chiaro che la DOA ha interesse solo per il cacciatore il quale non può di certo mettersi a misurare la distanza a cui si trova il capo di selvaggina e pretende solo di colpire più o meno dove ha mirato, senza preoccuparsi della curvatura della traiettoria. Se invece si spara ad un bersaglio ad una distanza ben definita, l'arma deve comunque essere azzerata per detta distanza affinché l'errore di puntamento non sia eccessivo e non si cumuli con gli altri fattori di dispersione del tiro.
In alcune tavole anglosassoni è indicata anche una distanza ottimale di azzeramento a breve distanza (10-30 metri) il cui significato sarà subito chiaro osservando la figura I: siccome la traiettoria incontra due volte la linea di mira, invece di azzerare l'arma rispetto al punto DOA, è possibile azzerarla al punto dove la traiettoria incontra la linea di mira per la prima volta; ciò può tornare utile quando non si disponga di una sufficiente distanza sul poligono e ci si accontenta di una prima taratura approssimativa.
Giova ricordare che i dati più attendibili forniti dalle tabelle sono quelli relativi ai tempi di volo, facilmente misurabili, ed alle velocità residue alle varie distanze; invece le ordinate progressive in genere non vengono misurate, ma sono calcolate e spesso risentono di errori derivanti dal sistema di calcolo usato.
Per eseguire calcoli relativi ad una data traittoria utile, fino a circa 500 metri, occorre apprendere come sia possibile integrare ed estendere i valori tabellati.
Nei calcoli che seguono abbiamo sempre preso come base i dati della tabella del proiettile 7x64 HMK della RWS.

Calcolo dei tempi di volo intermedi
Il tempo di volo è dato dal rapporto tra spazio percorso e velocità

t = s/v

ove v sta ad indicare la velocità media del proiettile nel tratto in questione. Una sufficiente approssimazione si ottiene assumendo come velocità media la velocità a metà percorso così che il tempo di volo a 100 metri sarà dato da 100 diviso per la velocità a 50 metri, quello a 150 dividendo 150 per la velocità a 75 metri, ecc.
Ad esempio dovendosi cacolare il tempo di volo a 200 metri, si dividerà 200 per la velocità a 100 metri di distanza, pari a 765 m/sec, ottenendosi t = 0,261 sec (in tabella 0,260).
Se la velocità a metà percorso non è nota, potrà usarsi il valore ottenuto facendo la media tra valore iniziale e finale sul tratto.
Ad esempio il tempo di volo per la distanza di 75 metri si otterrà dividendo 75 per la media tra 805 e 765 (= 785 m/sec), ottenendosi t = 0,095 sec.

Nota: la media può essere aritmetica (sommare i due valori e dividere il risultato per due) oppure geometrica (moltiplicare i due valori ed estrarre la radice quadrata). Un valore perfetto può ottenersi trovando le due medie, facendo la media aritmetica e la media geometrica dei due valori trovati e così via, finché i due valori coincidono.

Calcolo delle velocità noti i tempi di volo
Questo sistema è dovuto a W. Weigel e, oltre ad essere molto preciso, è veramente utile al comune sperimentatore poiché il tempo di volo alle varie distanze è il dato più facilmente misurabile con gli apparecchi elettronici in commercio. La precisione ottenibile dipende evidentemente dalla esattezza dei dati a disposizione e quindi, per quanto possibile, si deve evitare di ricorrere a data interpolati, quali quelli ottenuti nell'esempio precedente.
Il Weigel parte dalla considerazione che la perdita di velocità in un determinato tratto della traiettoria dipende dal coefficiente balistico del proiettile e dalla velocità a metà di essa; così, ad esempio, il calo di velocità da V50 a V100 è calcolabile in funzione di V75;
ogni differenza di velocità tra due punti simmetrici rispetto alla distanza di 75 m sarà esprimibile in funzione della stessa V75. Si potrà quindi scrivere, ad esempio

Vo - V150 = 3 (V50 - V100)

e così via.

Se ora noi disponiamo dei tempi di volo a 100-200-300 metri, possiamo già calcolare direttamente tre velocità a 50-150-250 metri e cioè:

V50 = 100/0,123 = 813 m/sec

V150 = 100/ (0,260 - 0,123) = 729 m/sec

V250 = 100/ (0,411 - 0,260) = 662 m/sec
Per il punto intermedio di 125 m. si potrà egualmente scrivere

V50 - V200 = 3 (V100 - V150)

e per il punto intermedio di 175 metri:

V100 - V250 = 3 (V150-V200)

E da queste relazioni si ricava

V100 = (3V50 + 6V150 - V250) / 8

Nell'esempio sarà quindi

V100 = (3·813 + 6·729 - 662) / 8 = 768 m/sec
V200 = (6V150 + 3V250- V50) / 8 e quindi
V200= (6·729 + 3·662 - 813) / 8 = 693 m/sec
V0 = 3 (V50 - V100) + V150
V0 = 3·(813 - 768) + 729 = 864 m/sec
V25 = (3V0 + 6V50 - V100) / 8
V25= (3·864 + 6·813 - 768) / 8 = 837 m/sec
V300 = V100 - 2(V150 - V250)
V300 = 768 - 2(729 - 662) 634 m/sec
V400 = V0 - 2(V100 - V300)
V400 = 864 - 2·(768 -634) = 596 m/sec
V500 = V0 - 5(V200 - V300)
V500 = 864 - 5·(693-634) = 569 m/sec
Sarà perciò possibile, noti solo tre tempi di volo del proiettile, risalire con una buona approssimazione alle velocità dello stesso per vari tratti dell'intera traiettoria venatoria.

Calcolo di velocità intermedie
Qualora siano noti V0, V150 e V300, si può ricorrere al metodo consigliato da W. Lampel che consente di calcolare le velocità intermedie di 50 in 50 metri con sufficiente approssimazione per i proiettili standard usati per caccia.

Siano ad es. V0 = 850 m/se; V150 = 735 m/sec e V300 = 620 m/sec e si calcolino del differenze:

V0 - V150 = 125

V150 - V300 = 105

Si calcolino ora

a = 37% di 125 = 46,25

b = 70% di 125 = 87,5

c = 36% di 105 = 37,8

d = 69% di 105 = 72,45

Sarà poi

V0 - a = 850 - 46 = 804 (V50)

V0 - b = 850 - 87,5 = 762 (V100)

V150 - c = 725 - 37,8 = 687 ( V200)

V150 - d = 725 - 72,45 = 620 (V300)

con buona corrispondenza ai valori tabulati.

Tracciamento di una traiettoria venatoria qualsiasi
Non sempre si dispone dei dati relativi alla traiettoria di un proiettile, oppure può essere necessario calcolare una traiettoria per un punto di azzeramento ed una linea di mira diversi da quelli indicati nelle tavole commerciali.
Un sistema molto valido è quello proposto da F. Avcin il quale calcola le ordinate progressive della traiettoria in relazione ai tempi di volo secondo la formula

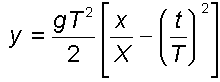
in cui X è la distanza di azzeramento, T il tempo di volo a tale distanza e t il tempo di volo alle varie distanze x a cui calcolare l'ordinata.

Si voglia, ad esempio tracciare la traiettoria del proiettile preso ad esempio, con arma azzerata a 300 metri.

Le ordinate progressive saranno date da

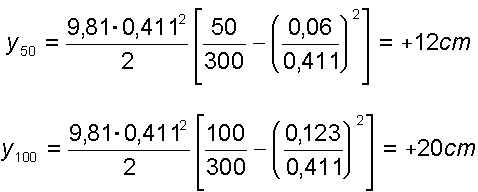
e così via ottenendosi
y150 = + 23,7 cm
y200 = + 22 cm
Se si calcola anche il tempo di volo per 350 metri, pari a 0,503 sec., si potrà calcolare anche l'ordinata la per
y350 = - 27,4 cm (negativa in quanto al di sotto della linea di sito).
I valori così trovati e riportati in un grafico come in fig. II, consentiranno di tracciare la traiettoria voluta. Naturalmente per le ordinate occorre scegliere una scala treo quattro volte maggiore di quella usata per le ascisse (cioè per rappresentare le distanze).

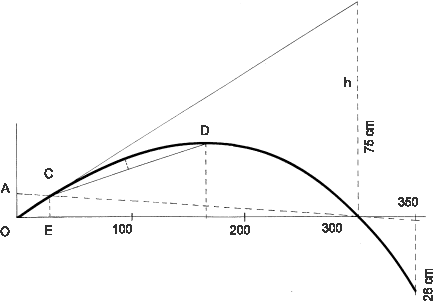
Figura II

Supponendo ora che si spari con un cannocchiale la cui linea di mira si trovi 5 cm sopra l'asse della canna, sarà sufficiente riportare la misura di 5 cm al di sopra di O nel punto A; la linea congiungente il punto A con il punto di azzeramento, rappresenta la linea di mira attraverso il cannocchiale e da essa potranno misurarsi le varie distanze dalla traiettoria e cioè le ordinate progressive rapportate alla linea di mira in considerazione.
Le ordinate progressive rispetto alla linea di mira si ottengono, matematicamente, sottraendo dal valore trovato rispetto alla linea di sito, la quantità data dalla formula

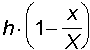
in cui h indica l'altezza dell'asse del congegno di mira sopra la linea di mira, in metri; ad esempio per h = 0,05 m e y100 = + 0,20 m, si avrà

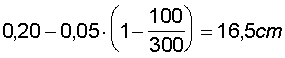
come si può misurare dal grafico.
L'ordinata al vertice della traiettoria può essere letta dal grafico. Per cartucce da caccia aventi traiettoria tesa, si può assumere che essa sia posta poco oltre la metà della gittata e cioè

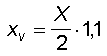
e quindi, nell'esempio, Xv=(300/2)·1,1 = 165 m.

Alla distanza Xv perciò, la distanza della linea di mira dalla linea di sito si è ridotta circa alla metà e si può quindi accettare la regola empirica secondo cui l'ordinata massima della traiettoria riferita alla linea di sito è pari all'ordinata sopra la linea di mira a metà gittata, aumentata della metà dell'altezza della linea di mira. Perciò se in tabella si legge che l'ordinata a 150 m è eguale a +17 cm sopra la linea di mira con cannocchiale di 5 cm, l'ordinata massima rispetto alla linea di sito sarà pari a 17 + 5/2 = 19,5 cm (in figura due esso è pari a cm 22, valore da ritenersi più esatto rispetto a quello ottimistico della tabella).
Se ora dal punto C si traccia quella corda alla curva che non disti da essa più di 4 cm, si otterrà il punto D, la cui ascissa individua esattamente la distanza ottimale di azzeramento (DOA), pari, nella figura a 161 m.
Infine la distanza OE indica la distanza a cui la traiettoria taglia per la prima volta la linea di mira (distanza breve di azzeramento), pari a m. 20.
La distanza tra la linea di mira e la traiettoria a 350 metri (pari nell'esempio a 26 cm), ci dice che sparando con l'arma azzerata a 300 metri contro un bersaglio che invece si trova a 350 metri, si commette un errore di ben 26 centimetri.

Angolo di proiezione
Tracciando la tangente alla traiettoria all'origine O e abbassando da essa la perpendicolare al punto di caduta, questa perpendicolare misura lo spazio di caduta h del proiettile alle varie distanze. Da questo valore si ricava direttamente l'angolo di proiezione applicando la semplice formula trigonometrica

Nell'esempio sarà tangf = 0,75/300, da cui l'angolo sarà 0° 8, 35,66".

Dalla figura I si rileva che l'angolo di proiezione è opposto al vertice, e quindi eguale, all'angolo formato dalla linea di proiezione con la linea di mira. Supponendo che la linea di mira sia posta a 5 cm sopra l'asse della canna, la distanza breve di azzeramento sarà data direttamente dalla formula 0,05/tangf = 20 m, come già ricavato dal grafico.

Caduta del proiettile rispetto alla linea di proiezione
La caduta del proiettile h, sopra calcolata, tiene conto del fatto che nell'atmosfera la caduta del proiettile viene rallentata dalla resistenza dell'aria e da una certa portanza del proiettile, così che essa è sempre inferiore a quella che si avrebbe nel vuoto. Nel vuoto infatti la caduta sarebbe stata data dalla formula h = (g·T²)/2 e sarebbe stata pari a 83 cm invece dei 75 reali. Da questo fenomeno deriva la difficoltà di calcolare con sistemi semplici la traiettoria di un proiettile, pur essendo nota la sua legge di resistenza, perché la diminuzione della componente rappresentante la forza di gravità, variabile in relazione a molti fattori, produce un aumento della gittata rispetto a quella che si otterrebbe supponendo che la caduta avvenisse secondo la legge valevole per il vuoto e, in misura minore, supponendo che la caduta avvenisse verticalmente nell'aria.
In via alquanto approssimativa, la caduta del proiettile nell'aria può essere calcolata adottando coefficienti di correzione della forza di gravità.
Il primo coefficiente è quello proposto dal Siacci, valido per gittate piuttosto brevi e tese, e fornito dalla formula

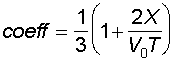
Nell'esempio si avrebbe

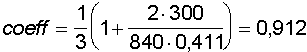
Se ora moltiplichiamo 83 cm per 0,912, otteniamo proprio il valore di 75, 5 cm (naturalmente si poteva anche inserire il valore di 9,81·0,912 = 8,9 come valore di "g" nella formula della caduta nel vuoto).
Il secondo è stato proposto da Mc Shane-Kelly-Reno ed è espresso in funzione del rapporto R = Vc/Vo in cui Vc indica la velocità alla distanza considerata;
il valore della gravità sarà dato dalla formula

g = 5,126 + 6,337R - 1,65R²

Nell'esempio si avrebbe R = 620/840 = 0,738 e g = 8,9 come con la formula di Siacci.

Distanza di azzeramento di armi militari
In tempi moderni i fucili militari non vegono azzerati secondo criteri venatori di precsione, ma con un criterio tattico in modo da garantire di colpire un bersaglio umano in un punto vitale, senza troppo mirare (Battlefield Zero o Point Blank Range). in esso si parte dala considerazione che il bersaglio vitale abbia un diametro di 30 cm e che sia utile la traiettoria che non di discosta più di 15 cm dalla linea di mira.Perciò mentre, ad es. per un proiettile 5,56x45 con Vo 850 ms la DOA (GEE) è a 173 metri con uno scostamento massimo di 5 cm dalla linea di mira e una distanza breve di azzeramento di 48 m. adottano la taratura militare si ha una distanza di azzeramento a 245 metri (distanza breve 30 m) con la massima altezza della traietotria di 15 cm a 160 m. Il proeittle raggiungera i 15 cm al di sotto della linea di mira a 300 metri.