Balistica terminale

La balistica terminale studia il comportamento del proiettile nel bersaglio. Qui ci occuperemo solo di quei pochi problemi di balistica terminale che possono essere oggetto di una valutazione matematica, riservando ad un'altra voce la trattazione dei fenomeni attinenti piuttosto alla medicina legale.
Uno dei fenomeni che meglio si presta ad uno studio scientifico è quello della penetrazione del proiettile nei vari mezzi, pur considerando che la diversità dei materiali e la diversità di comportamento dei singoli proiettili, a seconda della loro struttura e della velocità al momento dell'impatto, non consentono il ricorso ad un modello matematico generale, ma soltanto a formule empiriche. Accade infatti, da un lato, che proiettili ad alta velocità si deformino facilmente all'impatto e, d'altro lato, che proiettili molto veloci non facciano a tempo a trasferire la loro energia al bersaglio.
Punto di partenza per calcolare la penetrazione del proiettile nella maggior parte dei materiali è la sua energia cinetica o forza viva; essa può essere calcolata con la formula

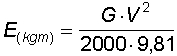
in cui G rappresenta il peso in grammi e V la velocità in m/s. Se si elimina il valore 9,81 si ottiene il risultato in Joule (1kgm = 9,81 J). Qui trovate un piccolo programma per il suo calcolo in Joule..
Le formule che proporremo sono state elaborate per proiettili di pistola incamiciati ed a punta tondeggiante e presuppongono un impatto sul bersaglio ad angolo retto. Se il proiettile colpisce il bersaglio con un angolo minore, il che può accadere per effetto dei movimenti di precessione, anche se il piano del bersaglio è perpendicolare alla traiettoria), la sua capacità di penetrazione sarà naturalmente minore fino a giungere, oltre un certo angolo, al rimbalzo.
Nell'attraversare materiali in più strati può anche accadere che il proiettile, che inizia a penetrare già inclinato, venga ulteriormente deviato nell'attraversamento del primo strato, così da non essere più in grado di attraversare il secondo su cui scivola semplicemente (è all'incirca il fenomeno per cui un raggio di luce viene rifratto quando dall'aria penetra nell'acqua). In linea di massima i risultati ottenibili con le formule sono utilizzabili anche per proiettili di carabina e per proiettili non incamiciati in quanto lo scarto nella penetrazione rispetto al proiettile tipo, se non intervengono deformazioni, può assumersi come costante e lineare e quindi facilmente verificabile in via sperimentale; ad esempio si riscontra sperimentalmente che la penetrazione di proiettili di piombo nel legno o nel ferro è inferiore di circa il 20% rispetto a quella di un proiettile incamiciato di eguale calibro. Particolare cautela occorre nell'applicare le formule a proiettili semicamiciati, proprio per la grande varietà di deformazioni che possono subire. Nelle formule che seguito i simboli sono usati, salvo diversa indicazione, con il seguente significato:
P: penetrazione in cm riferita alla punta del proiettile
E: in chilogrammetri
V: velocità di impatto in m/s
G: peso in grammi
C: calibro in mm.
S: sezione del proiettile in cmq

Penetrazione nel ferro
La penetrazione di proiettili nel ferro (blindature, carrozzerie, ecc.) è stata oggetto di ampi studi in campo militare e la formula più usata è quella di Krupp

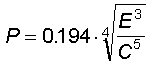
con cui possono risolversi problemi quali:
- un proiettile di pistola cal. 9 Para può perfora la blindatura di un'auto a 100 metri di distanza?
- quale velocità possiede il proiettile dopo aver perforato una lamiera di un millimetro?

Si badi che la formula di Krupp è valida solo per l'attraversamento di uno strato omogeneo di metallo; ad esempio un proiettile cal 9 Para perfora alla velocità di 330 m/s una piastra di circa 2,1 mm di spessore o tre piastre da 0.7 mm pressate assieme; se invece le tre piastre sono distanziate l'una dall'altra, ad es. di un centimetro si assiste al fenomeno un po' paradossale ma scientificamente spiegabile, per cui ne perfora ben 15 per un totale di 10,5 mm ! Si veda apposita voce La perforazione di lastre sottili

Penetrazione nel legno
La penetrazione nel legno di abete è presa comunemente come indice dell'efficacia di un proiettile. Essa può essere calcolata con la formula di Weigel

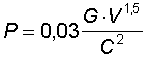
oppure con quella di Hatscher che ha il vantaggio di tener conto del fattore di forma i, il che è utile specialmente per proiettili di fucile

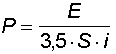
Penetrazione nell'osso

La formula che per proiettili idi pistola incamiciati fornisce i migliori risultati è

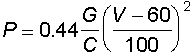
Per proiettili a punta arrotondata si deve sostituire la costante 0,44 con 0,30 e per proiettili wad-cutter con la costante 0,15.

Dalla velocità al momento dell'impatto vengono detratti 60 m/s che rappresentano la perdita di velocità per effetto del solo impatto; ciò significa, in altre parole, che un proiettile con velocità inferiore a 60 m/s produce sull'osso solo un effetto contusivo, ma non ne spezza il tessuto. Questa cosiddetta velocità limite di 60 m/s è riferita a proiettili per pistola a punta tondeggiante o a palle sferiche; nel caso di proiettili con elevata densità sezionale oppure molto appuntiti, è chiaro che la velocità limite sarà inferiore. Se il proiettile attraversa altri tessuti (indumenti, muscolo), bisognerà ovviamente tenerne conto.
Il Sellier fornisce anche la formula per calcolare la perdita di velocità al passaggio di un certo spessore di osso. La formula è
Vr = Velocità residua
Vo = Velocità operante dopo aver tolto i 60 ms liminari
Calibro in cm
Peso in grammi
S spessore osso perforato in cm

Ad esempio se un proiettile C = 0,635 di P = 3,2 gr inizia a lavorare sull'osso a 120 m/s , nel perforare 0,5 cm perderà 10 m/s (esempio del Sellier).

Penetrazione nella cute
Il limite di velocità a cui un proiettile è ancora in grado di bucare la cute umana è stata studiata per proiettili di pistola o per palle sferiche e risulta valida la formula del Sellier

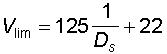
in cui Ds rappresenta la densità sezionale. Questa è data dal rapporto G/S.
Dalla formula si ricava, ad esempio, che un pallino da caccia di 3 mm di diametro non riesce a perforare la pelle, ma procura solo una contusione, se non raggiunge la velocità di 78 m/s.
La stessa formula può essere usata anche per indumenti; sostituendo il valore +100 a +22 si ha la velocità limite per la tuta da combattimento americana a sei strati di tessuto.

Il Kneubuehl ha successivamente ridefinito il concetto di velocità limite, come quella del proiettile (o scheggia) che con grande probabilità su di un corpo nudo non provocherà alcun danno, individuando quindi l’energia limite in 0,1 J/ mm² per la cute e in 0,06 J /mm² per l’occhio. L’esperienza insegna che un giocattolo soft-air può provocare danni all’occhio di un bambino già con 0,025 J /mm².
Si ottiene quindi la seguente tabella.

Si tenga presente che un proiettile pesante con Energia superiore a 4 J provoca comunque un ematona.
Per ottenere valori di sicurezza non si dovrebbe superare la metà del valore di E indicato in tabella.

Penetrazione nei tessuti molli del corpo umano
Sulla base di studi compiuti sulla gelatina balistica il Sellier è pervenuto alla formula

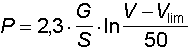
in cui dalla velocità di impatto V viene detratta la velocità limite relativa alla cute, il cui spessore viene però computato come spessore di tessuto muscolare
Le formule sopra riportate non sono solamente delle curiosità matematiche, ma possono orientare nella soluzione di problemi di balistica giudiziaria, di cui si riportano alcuni esempi.
1) Un uomo è stato colpito da un colpo di pistola da circa 100 metri di distanza che ha forato il cranio da parte a parte per complessivi cm. 1 di osso; è possibile che sia stata usata una cal. 7,65 ACP?
Un tale proiettile con velocità iniziale di 285 m/s, a 100 metri ha ancora una velocità di 240 m/s. Le perdite di velocità che subisce all'impatto sono di 35 m/s per impatto con la cute e di 60 m/s per l'impatto sull'osso; 10 m/s li perde nella perforazione dei primi 5 mm. di osso ed entra quindi nel cervello alla velocità di 135 m/s; a questa velocità perfora 12 cm di tessuti molli perdendo altri 35 m/s; ulteriori 60 m/s li perde all'impatto con la parete opposta del cranio e altri 10 m/s per la sua perforazione. Residuano quindi solo 30 m/s, proprio al limite della possibilità della completa perforazione (sperimentalmente si è accertato che da distanza ravvicinata solo l'80% dei proiettili cal 7,65 perfora il cranio da parte a parte; è quindi possibile, ma improbabile che vi sia riuscito a 100 metri di distanza).

2) Una persona viene colpita da un colpo cal. 9 Para da circa 100 metri di distanza, con perforazione della colonna vertebrale e fuoriuscita dalla parte opposta. È sufficiente un colpo di pistola (V= 280 m/s) o deve ipotizzarsi un colpo di mitra (V= 400 m/s) ?
Le perdite di velocità sono di 60 m/s per impatto e attraversamento cute ed abiti, 60 m/s per impatto con l'osso spesso 2 cm, 20 m/s per la sua perforazione; rimangono solo 140 m/s insufficienti per perforare tutto il ventre e la cute e gli abiti nella parte anteriore; deve quindi ipotizzarsi che il colpo sia stato sparato con un mitra.
Attenzione; nel fare questi calcoli attenzione a non sottrarre due volte la velocità limite!

Penetrazione in materiali vari
Per il calcolo della penetrazione in vari materiali, quali terra o mattoni, si può usare la formula di Petry in cui P è il peso in gr, C il calibro in mm, V la velocità di impatto in ms e k un coefficiente con il seguente valore

0,016	Acciaio
0,025	lega di acciaio
0,64	muro di cemento
0,94	muro di pietra
1,63	muro di mattoni
2,29	terreno sabbioso
3	terreno normale erboso
0,336	pietra calcarea
4,565	terreno soffice
5,87	terreno argilloso

La formula richiede che lo spessore totale del materiale sia almeno tre volte quello calcolato; se è inferiore, la penetrazione aumenta.
La penetrazione Pn ( o D) in cm sarà data da

Quale riscontro si tenga presente che per un proiettile di pistola cal 7,65, la penetrazione in terra sabbiosa sarà di circa 17 cm. Qui trovate un piccolo programmino per eseguire il calcolo.

Penetrazione sperimentale in cm del proiettile militare 30-06 (Vo =845 m/s, P= 9,7 g) alla distanza di 180 metri

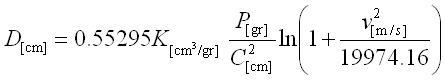
                            media          massima

Ghiaia                   17,7             20
Muro di mattoni    11               16.5

Sabbia asciutta      18,5            20,7
Sabbia bagnata     18,5             23,3
Argilla                   62               73,5
Terra sciolta          50               50

Per la balistica terminale del pallino si veda la pagina sulla rosata