L'ESPLOSIONE
2.1 - L'esplosione è un fenomeno di trasformazione chimica o chimico-fisica che avviene in un tempo rapidissimo, accompagnata da sviluppo di energia (per buona parte termica) e, in genere, da sviluppo di gas.
Qualsiasi sistema che per somministrazione di piccolissime quantità di energia termica o meccanica è capace di trasformarsi chimicamente, in un tempo brevissimo, con sviluppo di energia, di gas e di vapori, costituisce un
sistema esplosivo. Un sistema esplosivo è
omogeneo se costituito da una sola specie chimica definita e invece
eterogeneo quando è costituito da più sostanze chimiche.
Gli esplosivi sono quindi sostanze ad alto contenuto energetico, che, attraverso l'esplosione, si trasformano in sostanze stabili, a contenuto energetico molto inferiore. Gli esplosivi
solidi sono miscele o combinazioni solide suscettibili di assumere il regime di
detonazione; si riserva il nome di
polveri agli esplosivi che assumono il regime
di deflagrazione.
I gas prodotti dalla reazione, a causa delle altissime temperature raggiunte nell'esplosione, tendono ad occupare volumi enormemente superiori a quelli corrispondenti alle sostanze di partenza. Se quindi una certa quantità di esplosivo esplode quando è racchiusa in un ambiente ristretto, i gas provocano sulle pareti una pressione istantanea ed elevatissima che, qualora la resistenza delle pareti non sia adeguata, ne provocherà la rottura: su questo principio è basato il funzionamento delle mine.
DEFLAGRAZIONE E DETONAZIONE
2.2 - Gli esplosivi che interessano la nostra trattazione sono in genere sostanze solide che contengono ossigeno, azoto ed elementi combustibili.
I primi combustibili usati sono stati C e S; di recente insieme al C è stato introdotto anche H attraverso sostanze organiche (vasellina, paraffina, amido, zucchero, segatura di legno, farina di cereali, ecc.). Il modo con cui gli elementi anzidetti sono contenuti negli esplosivi è indicato al n. 3.1; si accenna qui che all'atto dell'esplosione il C si combina con l'O per formare CO
2 e CO, entrambi gassosi; che 1'H si combina con l'O per formare vapore d'acqua, che 1' N si libera come tale o che si combina a NO e NO
2 ; che nei gas possono trovarsi ancora (a seconda della formula degli esplosivi) CI, HCI, H
2S, ecc.
Alcune sostanze possono bruciare semplicemente od esplodere a seconda di come sono costrette nell'ambiente; basta pensare alla benzina, la quale brucia in una lampada da saldatore e invece esplode nei cilindri delle macchine a scoppio. Così pure molte reazioni chimiche si sviluppano con velocità differenti in conseguenza di vari fattori: temperatura, concentrazione dei reattivi, presenza di adatti catalizzatori. In conseguenza alcune reazioni possono verificarsi in forma normale o in forma esplosiva.
Si chiamano
velocità esplosive quelle corrispondenti a tempi brevissimi, inferiori a quelli necessari affinché il calore di reazione possa trasmettersi al mezzo circostante per conduttività e irraggiamento e che quindi si accumula nei gas prodotti, allo stato di energia cinetica.
Le velocità esplosive sono sempre alte ma possono variare fra loro anche di molto. Le esplosioni che avvengono alle velocità inferiori si chiamano
deflagrazioni (dette anche
esplosioni di primo grado), quelle corrispondenti alle velocità alte si chiamano
detonazioni (o esplosioni di secondo grado).
Però la differenza fra deflagrazione e detonazione non risiede solo nella velocità con cui procede il fenomeno, bensì si tratta di due sistemi di propagazione sostanzialmente diversi.
La deflagrazione è un fenomeno esplosivo che si propaga per conduttività termica iniziando alla superficie esterna della massa (in genere dei granuli) e procedendo verso l'interno. La durata della reazione è inferiore per polveri a graniture fini (che hanno maggior superficie per unità di peso) per cui alle diverse graniture corrispondono diverse velocità di deflagrazione. Queste velocità sono però sempre molto inferiori di quelle di detonazione e in conseguenza sono meno importanti gli effetti distruttori (naturalmente a parità di massa).
La detonazione è un fenomeno così violento che non può essere spiegato solo con il meccanismo della combustione ed infatti essa si propaga con il meccanismo
dell'onda esplosiva. In detta onda (il cui nome e definizione sono dovuti a Berthelot) sono associati un fenomeno fisico
(onda di pressione o
onda d'urto) e un fenomeno chimico
(reazione di combustione, detta anche
onda di combustione); i due fenomeni si sostengono a vicenda per cui sulla fronte dell'onda esplosiva coesistono l'onda d'urto e la reazione chimica.
Le espressioni « onda esplosiva », « onda di detonazione » e « detonazione » sono sinonimi.
Per inciso si fa osservare che la detonazione non è necessariamente un fenomeno di combustione: ad esempio l'azotidrato di piombo nella detonazione non segue un meccanismo di ossidazione, ma una reazione di decomposizione.
Nell'esplosione di miscele gassose si definisce
periodo d'inizio o inizio della detonazione l'intervallo di tempo compreso fra l'istante in cui la miscela si accende e l'istante in cui ha inizio l'onda esplosiva. Durante questo periodo la velocità della fiamma cresce molto rapidamente fino a raggiungere la velocità dell'onda esplosiva; un periodo di inizio analogo si presenta nella detonazione degli esplosivi solidi.
Le velocità di deflagrazione sono in genere dell'ordine delle centinaia di metri al secondo, le velocità di detonazione sono comprese fra più di 1000 e circa 9000 m/s. Si avverte che però i limiti di velocità di deflagrazione non sono bene precisabili perché dipendono da vari fattori: infatti oltre alla granitura delle polveri hanno influenza l'entità dell'innesco, la densità della carica, il diametro della carica, ecc.
2.3 - In dipendenza di alcuni fattori, primo fra i quali la violenza dell'urto iniziatore, la deflagrazione può tramutarsi in detonazione e così un esplosivo normalmente deflagrante, come è la polvere nera, può detonare quando è fortemente innescato; viceversa la dinamite (detonante) può deflagrare se stimolata con un innesco troppo debole. Infatti gli esplosivi da mina, anche se pulverulenti, reagiscono secondo una legge analoga a quella che Muraour ha stabilito per la combustione degli esplosivi colloidali:
V=a+bp
nella quale
V = velocità di combustione;
a e
b = coefficienti dell'esplosivo; p = pressione.
La formula mostra la proporzionalità fra velocità e pressione e spiega perché sostanze che bruciano poco o nulla all'aria alla pressione ordinaria possono bruciare rapidamente, e anche esplodere, quando sono molto compresse.
2.4 – È pericoloso che un esplosivo deflagrante detoni, ma lo è anche che un esplosivo detonante deflagri, perché in questo caso avvengono anomalie nel funzionamento delle mine. Può infatti aversi in quest'ultimo caso:
1) accensione ritardata - al momento del brillamento non si sente il colpo dell'esplosione, che infatti si verifica con un certo ritardo;
2) detonazione doppia - al momento del brillamento si ode un colpo, seguito da un altro con un certo ritardo;
3) fiammata o fuoco - il colpo non è partito e la mina non ha provocato caduta di materiale, ma dal foro esce fumo e talvolta anche fiamma.
Questi inconvenienti sembrano dovuti al fatto che tutta la carica, o una parte di essa, non avrebbe raggiunto il regime di detonazione, ma avrebbe preso il regime della deflagrazione, bruciando con velocità relativamente lenta.
Queste irregolarità disturbano il lavoro e sono pericolose, specie in carbone, in quanto può derivarne un incendio, e più ancora in ambiente grisutoso per il pericolo di esplosione del grisù stesso.
Gli esplosivi deflagranti sono ad azione relativamente lenta, quelli detonanti sono ad azione più rapida. Ne discende che un esplosivo deflagrante sarà preferibile quando si vuole ottenere un effetto di spinta e non frantumare troppo il materiale da abbattere; che viceversa occorrerà un esplosivo detonante quando si vogliono imprimere alla massa azioni violente, demolitrici.
CARATTERISTICHE DEGLI ESPLOSIVI INDUSTRIALI
E PROVE RELATIVE
Composizione chimica
2.5 - La composizione chimica di un esplosivo è definita dalla sua formula (bruta o di struttura) dalla quale si deducono il peso molecolare e la percentuale degli elementi che entrano nella composizione.
Per la nitroglicerina (cfr. n. 3.2), di formula C
3H
5 (ONO
2)
3 il peso molecolare risulta
di 227 e la proporzione dei componenti (in %): 15,8 C; 2,2 H; 18,5 N; 63,5 O.
Stato fisico
2.6 - Lo stato fisico degli esplosivi è anche un criterio per la loro classificazione. Si rimanda quindi al n. 3.1.
Bilancio di ossigeno
2.7 - L'ossigeno negli esplosivi non è indispensabile (e infatti alcune famiglie di esplosivi non lo contengono) però esso è presente in quasi tutti gli esplosivi e il suo ruolo è molto importante in quanto nell'esplosione una molecola ossigenata si scinde in altre molecole più semplici con liberazione di energia termica.
La capacità ossidante dell'ossigeno dipende non tanto dalla sua proporzione quanto dalla struttura della molecola dell'esplosivo: se l'ossigeno nella molecola è già associato all'H e al C in combinazioni stabili esso non ha più valore agli effetti di reagire con essi, cosa invece possibile quando il legame è labile, come è quello dell'O con il gruppo NO. Si può
distinguere la percentuale di
ossigeno totale da quella di
ossigeno attivo, ma ancora i dati non sono significativi in conseguenza dei diversi tipi di legami che esso ha nella molecola con il C e con l'H:
infatti, data la rapidità dell'esplosione, l'O che viene consumato nella reazione è solo quello interno delle molecole di esplosivo, nella cui composizione entrano normalmente anche l'idrogeno, il carbonio, l'azoto. Se l'O nell'esplosivo, è sufficiente per ossidare tutto il C a CO
2 e tutto 1'H ad H
2O l'esplosivo è detto ad
esplosione completa e si
parla di
bilancio di ossigeno nullo. Di questo tipo è l'esplosione del nitroglicol :
C2 H4ON2 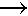 2CO2 + 2 H2O + N2
2CO2 + 2 H2O + N2
Ci sono esplosivi che contengono ossigeno esuberante per la reazione, nel qual caso resta ossigeno libero nei prodotti della reazione. Ad esempio la nitroglicerina esplode secondo la reazione
4C3H5 (ONO2 )3 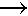 12CO2 + 10H2O + 6N2 + O2
12CO2 + 10H2O + 6N2 + O2
si dice che il bilancio di ossigeno di questo esplosivo è
positivo. In molti esplosivi viceversa l'O non è sufficiente per ossidare tutto il C e 1'H, per cui questi restano ossidati parzialmente o liberi. Così è per l'esplosione del trinitrotoluene (cfr. n. 3.6):
2C7H5 (NO2 )3 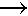 12CO + 5H2 + 3N2 + 2C
12CO + 5H2 + 3N2 + 2C
e allora il bilancio di ossigeno si dice
negativo.
Il bilancio di ossigeno quindi può essere definito come il
numero di grammi di ossigeno che mancano o eccedono rispetto alla combustione completa di 100 g di esplosivo.
Nell'esempio visto sopra, della nitroglicerina, di peso molecolare 227, per ogni molecola-grammo restano liberi 8 g di ossigeno, quindi si ha:
8 : 227 = x : 100
da cui
x = + 3,5%
Sono state pubblicate tabelle nelle quali è indicata la quantità di ossigeno necessaria per la combustione di ognuna delle sostanze impiegate nella fabbricazione degli esplosivi (Ad es. in: TAYLOR C.A., RINKENBACH W. H.,
Esplosives - Their material constitution and analysis, U.S.A. Bureau of Mines, Bulletin n. 219, 1923.)
Con esse è molto semplice calcolare il bilancio di ossigeno di un esplosivo: basta moltiplicare le quantità lette in tabella per le rispettive percentuali dei componenti e fare la somma algebrica.
Ad esempio per la gomma, di composizione 92,7 di nitroglicerina e 7,3% di cotone collodio, poiché l'ossigeno disponibile per 100 g di sostanza è rispettivamente + 3,5 e
- 44,4 si ha:
92,7 x (+ 3,5) = + 324,4
7,3 x (- 44,4) = - 324,1
quindi il bilancio di ossigeno di quella gomma è + 0,003%, ossia praticamente zero.
Si fa osservare che alcuni esplosivi (come ad esempio l'azotidrato di piombo)
nell'esplosione non comprendono reazione ossidante; così per essi non si può parlare di bilancio di ossigeno.
L'argomento del bilancio di ossigeno è ripreso più avanti.
Temperatura di esplosione
2.8 - È la temperatura massima che i gas prodotti raggiungono al momento dell'e splosione, a volume costante. Per gli esplosivi detonanti le temperature di esplosione (più propriamente di detonazione) oscillano fra 2500 e 6000 °C.
Questa temperatura non è misurabile direttamente perché i termometri non riescono a registrare una variazione così rapida, ma può essere calcolata partendo da considerazioni teoriche con buona approssimazione.
Calore (energia) di esplosione
2.9 - L'esplosione è un fenomeno esotermico, quindi nella reazione si libera una quantità di calore uguale alla differenza fra la somma dei calori di formazione delle sostanze generate dall'esplosione e la somma dei calori di formazione dell'esplosivo.
I calori di formazione vengono determinati a 20°C e a pressione costante, ma nel caso delle utilizzazioni pratiche degli esplosivi nelle mine la reazione avviene nell'ambiente del foro, che rimane a volume costante, quindi quello che interessa per gli esplosivi è il calore sviluppato a volume costante. Questo secondo calore è superiore al primo di una quantità corrispondente al lavoro speso per la dilatazione dei gas fino alla pressione atmosferica.
Il calore di esplosione viene calcolato facendo detonare alcuni grammi di esplosivo in una adatta bomba calorimetrica. Si assume il calore sviluppato nella detonazione di 1 g di esplosivo e le cifre che si ottengono sono molto modeste, comprese nell'intervallo da 400 a 600 kcal/kg, cifre inferiori a quelle corrispondenti dei normali combustibili.
La maggior parte degli esplosivi è ottenuta con la nitrazione (cfr. n. 3.1) di varie sostanze. Questi esplosivi sono relativamente poveri in energia perché il loro ossigeno è concatenato all'azoto nel radicale nitrico (i combustibili normali prendono l'ossigeno dall'atmosfera).
La stessa nitroglicerina ha il calore di esplosione a pressione costante uguale a 1512,8 kcal/kg, mentre la benzina brucia dando circa 11000 kcal/kg: un'automobile che funzionasse a nitroglicerina, ne consumerebbe quindi in peso circa 7 volte tanto.
Volume specifico (o volume normale) dei gas di esplosione
2.10 - È il volume occupato dai gas prodotti da 1 kg di esplosivo nelle condizioni normali (pressione di 760 mm di mercurio e 0°C di temperatura). Lo si può determinare facilmente con la bomba di pressione, ma è più facile partire dall'equazione di decomposizione. Bisogna però tenere presente che il valore dipende dalle condizioni pratiche in cui avviene la detonazione, avendo influenza la densità di carica e il tipo di innescamento di essa.
Per citare un esempio, la nitroglicerina ha un volume specifico di 715,6 1.
Volume dei gas di esplosione
2.11 - È il corrispondente del volume specifico alla temperatura di detonazione dell'esplosivo; in conseguenza della dilatazione dovuta allo sviluppo di calore il volume di detonazione è uguale a 10 - 15 volte quello specifico.
La nitroglicerina, di cui si è visto ora il volume specifico uguale a 715,6 1, ha il volume di esplosione uguale a 13.590 1.
Velocità di detonazione
2. 12 - Elementi che influenzano la velocità - La velocità dell'onda di detonazione ha lo stesso ordine di grandezza di velocità delle onde sonore attraverso i solidi e può essere calcolata attraverso l'equazione:
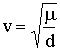
nella quale µ è il modulo di elasticità e d è la densità.
Al n. 2.2 si è visto che la velocità degli esplosivi deflagranti è in genere inferiore a 1000 metri al secondo e che quella degli esplosivi detonanti può raggiungere parecchie migliaia di metri; gli esplosivi con velocità superiore a quella dell'acido picrico (7000 m/s) si chiamano
ultradirompenti, o
anche
esplosivi nobili (la velocità massima appartiene alla miscela tetranitrometano-toluolo, con 9300 m/s).
La velocità di detonazione è una costante per esplosivi teorici, mentre oscilla alquanto per gli esplosivi pratici (anche a parità di tutte le condizioni) tanto che si parla talvolta di velocità di detonazione superiore e inferiore; questo però non ha grande importanza nella pratica industriale.
Viceversa bisogna conoscere l'effetto di altri fattori che influiscono sulla velocità di detonazione: temperatura, tipo di involucro o confinamento, diametro della cartuccia, densità di carica, entità e tipo dell'innesco, stato fisico e granulometria degli ingredienti, tipo dei componenti (con nitroglicerina o meno) e altri ancora.
Per ogni esplosivo esiste un diametro minimo
(diametro critico) al di sotto del quale si verifica una diminuzione di velocità così notevole, che l'effetto utile dell'esplosivo è praticamente annullato. Con esplosivi potenti basta il diametro di 10 mm per ottenere già la velocità massima, ma occorrono diametri maggiori per esplosivi meno sensibili.
La velocità di detonazione aumenta se la cartuccia è confinata entro un materiale resistente anziché essere libera nell'aria. Perdita di velocità notevole, con il pericolo di avere solo una detonazione parziale o semplice deflagrazione, si può avere se all'atto dell'esplosione un qualche punto della camera di scoppio cede prima che si sconnetta tutta la zona circostante; ecco perché è necessario chiudere bene il foro da mina con materiale di
intasamento che resista senza venir espulso alla pressione dei gas di scoppio.
Se l'innesco non è sufficientemente forte può non detonare tutta la carica e si può anche avere deflagrazione anziché detonazione.
Vale la pena di indicare che alcuni esplosivi, fra i quali figurano la nitroglicerina e le gelatine esplosive, presentano due distinte e stabili velocità di detonazione, molto diverse fra loro, dette rispettivamente
regime di bassa velocità e regime di alta velocità.
Ad esempio per le gelatine esplosive la velocità di basso regime oscilla fra 1500 e 2000 m/ s, quella di alto regime oscilla fra 6500 e 7500 m/s, in dipendenza del contenuto di nitroglicerina. Può anche verificarsi che l'esplosione cominci a basso regime e che a un certo momento la velocità diventi quello di regime alto. Quest'ultimo regime è quello che corrisponde a una reazione completa, con liberazione di tutta l'energia disponibile.
2. 13 - Saggio di Dautriche - La velocità di detonazione può essere determinata sperimentalmente. Un metodo semplice e pratico, dovuto a Dautriche, richiede soltanto una modesta attrezzatura. A una cartuccia dell'esplosivo da provare si fissano, vicino alle estremità, i due capi di un tratto di miccia detonante di una lunghezza che va misurata con esattezza e della quale deve essere nota con precisione la velocità di detonazione. La parte centrale della miccia, fatta girare intorno a un riparo, viene fissata sopra una sbarra di piombo, sulla quale si fa un segno in corrispondenza del punto mediano della miccia.
Innescando la cartuccia a una estremità e facendola brillare, detona prima l'estremità della miccia più prossima all'innesco indi l'altra estremità. Le due onde esplosive che percorrono la miccia in senso contrario lasciano una tacca sulla sbarra di piombo nel punto in cui si incontrano; allora misurando la lunghezza di cartuccia compresa fra i due attacchi della miccia detonante, lc, e la distanza della tacca dal punto mediano della miccia, 1m , mettendo in facile equazione i tempi impiegati dalla detonazione per percorrere il tratto di cartuccia lc , e la miccia, si ottiene:
Ve = V m * lc /2 lm
nella quale Ve è la velocità
incognita di detonazione dell'esplosivo e Vm è la
velocità di detonazione della miccia.
Si accenna che per la
determinazione anzidetta si può anche fare uso di sistemi elettronici. Si tratta di produrre due segnali elettrici, uno di avvio per un cronografo elettronico quando la detonazione interessa un punto prossimo all'estremità innescata di una cartuccia, e uno di arresto quando la detonazione
raggiunge un punto prossimo all'altra estremità della cartuccia: conoscendo la distanza fra i due punti e il tempo (che viene determinato con approssimazione superiore a un milionesimo di secondo) si ottiene la velocità di detonazione.
Durata della fiamma di esplosione
2.14 - È il tempo che impiega per estinguersi la fiamma dell'esplosivo ed è
quindi il rapporto fra la lunghezza della carica e la velocità di esplosione dell'esplosivo. Si tratta di tempi sempre molto brevi, ma c'è una escursione notevole fra vari tipi di esplosivi: da alcuni centomillesimi di secondo degli esplosivi rapidi e potenti si passa a circa 0,5 - 1 millisecondo degli esplosivi di sicurezza, a 1,5
secondi della polvere nera.
Questa caratteristica è
molto importante perché la temperatura di detonazione e la durata della fiamma hanno influenza sull'accensione del grisù
.
Lunghezza della fiamma di esplosione
2.15 - Anche la lunghezza della fiamma ha influenza sull'accensione del grisù.
Stettbacher (STETTBACHER A.,
Pólvoras y explosivos, Ed. Gili, Buenos Aires, 1952) ha misurato lunghezze di fiamma di 2 m per l'acido picrico, di 1,15 m per la polvere nera, di 0,1 m con la dinamite al 65% di nitroglicerina, di soli pochi centimetri negli esplosivi di sicurezza contro il grisù.
Pressione specifica (forza specifica)
2.16 - Per i gas ideali vale la legge di Clapeyron:
P = RT/V
nella quale P è la pressione, R la costante del gas, T la temperatura assoluta, V il volume. Per i gas reali la legge vale solo in prima approssimazione, ma inoltre c'è un'altra limitazione. Precisamente, la formula indica che la pressione è inversamente proporzionale al volume della camera di scoppio, il che si verifica con buona approssimazione alle pressioni normali, ma porta a risultati abbastanza diversi da quelli effettivi alle pressioni molto alte che si generano nel brillamento degli esplosivi.
In questi casi la proporzionalità inversa vale con un volume inferiore di quello della camera di scoppio e la formula precedente deve scriversi:
P = RT/(V – k) (formula 2.1)
La costante
k indica che per una pressione infinita
V - k = O, ossia che il volume potrà ridursi al minimo uguale a
k. Così
k è lo spazio minimo entro cui il gas può essere contenuto: lo si chiama
covolume. L'equazione è detta di
Sarrau. Applicandola al caso di due pressioni non molto differenti si può scrivere:
P 1 (V 1 - k) = P 2 (V 2 - k) (formula 2.2)
e
Amagat ne ha dedotto che per gli esplosivi normali il covolume di tutti i gas è uguale alla millesima parte del volume specifico, a temperatura e pressione normali, purché la pressione di esplosione non superi 4000 kg/cm² . Con queste limitazioni si può quindi scrivere:
k = 0,001 Vs (formula 2.3)
in cui Vs è il volume specifico.
Le considerazioni precedenti valgono quando tutti i prodotti della combustione sono gassosi. Se ci sono residui solidi, il loro volume va sommato a quello del covolume e la capacità della camera di scoppio ne può risultare diminuita in maniera sensibile.
Si è visto che il volume specifico degli esplosivi detonanti è di parecchie centinaia di litri; allora dalla (2.3) risulta che l'ordine di grandezza del covolume è di circa mezzo litro.
Ora si può definire la
pressione specifica, o forza specifica dell'esplosivo, come la pressione che si ottiene facendo brillare l'unità di peso di un esplosivo nell'unità di volume netta, ossia nel volume unitario più il covolume. Con altre parole, in pratica è la pressione che un chilo di esplosivo eserciterebbe esplodendo a volume costante in un recipiente avente capacità di un litro più il covolume di quell'esplosivo.
La forza specifica e il covolume si chiamano le
caratteristiche di Abel.
La forza specifica si calcola con la formula:
1 = 0,00378 Vs T
nella quale V, è il volume specifico espresso in litri; T è la temperatura di esplosione in gradi Kelvin.
Per la nitroglicerina, che ha Vs =
715,6 1, si ha:
f = 0,00378 x 715,6 x 3 780 = 10224,8
Si fa osservare che non si tratta di una forza nel senso della meccanica e che quindi essa non è espressa in chili, in quanto le dimensioni di
f sono quelle di una energia.
La forza specifica è proporzionale oltre che al volume specifico (come si è visto) anche alla temperatura di esplosione. Ciò significa che uno stesso valore di forza può essere ottenuto con alto volume specifico e temperatura relativamente bassa, oppure con volume specifico modesto ed alta temperatura: questo permette di scegliere esplosivi appropriati per vari usi (per esempio si possono così avere esplosivi di sicurezza contro il grisù abbastanza potenti).
Le pressioni che si raggiungono nella deflagrazione sono modeste ma diventano enormi quelle che si sviluppano nella detonazione. Queste ultime possono essere di 15000 - 20000 kg/cm² e con cariche sagomate e opportunamente preparate (cariche cave, cfr. n. 17.38) può superare di oltre 10 volte gli anzidetti valori.
La misura della pressione di esplosione viene fatta determinando lo schiacciamento di un cilindretto
(crusher) di rame, provocato da uno stantuffo spinto dall'esplosione di una piccola carica (alcuni grammi) di esplosivo entro una camera di acciaio.
I risultati che si ottengono sono abbastanza prossimi a quelli ricavabili per via teorica. Misure anche più precise possono essere ottenute con sistemi elettronici, che però sembra superfluo descrivere.
Lavoro prodotto, potenziale, potenza e dirompenza
2.17 Definizioni - Si è già visto, parlando del calore sviluppato dalle esplosioni, che le quantità di calore in gioco sono molte modeste, minori di quelle fornite dai combustibili ordinari. In conseguenza anche il lavoro prodotto è modesto, però esso viene sviluppato nel brevissimo tempo che dura l'esplosione e per questo gli effetti sono distruttori.
Il lavoro sviluppato da un chilo di esplosivo quando i gas dell'esplosione possono espandersi nell'ambiente secondo una adiabatica indefinita si chiama il
potenziale di quell'esplosivo. In altre parole il potenziale è l'equivalente in unità meccaniche del calore di esplosione; è quindi un valore convenzionale che esprime l'attitudine meccanica dell'esplosivo in esame.
Ad esempio per la nitroglicerina si è visto che il calore di esplosione è di 1512 kcal/kg, quindi il suo potenziale sarà:
1512,8 X 427 = 645965 kgm/kg
Però la brevità del tempo di esplosione consente che solo una parte del potenziale possa essere utilizzata: questa si chiama
potenza.
La potenza dipende dal volume dei gas sviluppati nell'esplosione (quindi dalla densità di carica) e dalla temperatura di esplosione, ma gli effetti di distruzione sono tanto maggiori per quanto più grande è la velocità di detonazione e così si considera là
dirompenza, la quale appunto tiene conto della velocità di detonazione ed esprime la maggiore o minore attitudine di un esplosivo a frantumare la roccia.
Per esprimere la dirompenza è usata la formula:
D = f d v10-6
nella quale
D = dirompenza, in cifra assoluta;
f = forza specifica; d = densità, in kg/l; v = velocità di detonazione, in m/s.
Questa formula, dovuta a Kast (che pose 10
-3 anziché 10
-6 ) dà valori convenzionali, ma atti per un confronto fra i vari esplosivi.
Ad esempio per la nitroglicerina, già avanti considerata, si ha f = 10224,8; d = 1,59; v = 7230; quindi:
D = 10 224,8 x 1,59 x 7 230 x 10-6= 117,5
La capacità dell'esplosivo di esercitare un effetto di rottura e di frantumazione sugli oggetti con esso a contatto al momento dell'esplosione prende anche il nome di
brisanza (dal francese briser = rompere). La brisanza ha avuto varie definizioni nel tempo; oggi si tende ad identificarla con la pressione di detonazione.
L'effetto utile di un esplosivo si esplica con due azioni fondamentali
l'azione di spinta (che dipende principalmente dalla pressione esercitata dalla massa gassosa) e
l'azione d'urto (dipendente in primo luogo dalla velocità di esplosione).
Il lavoro compiuto da un esplosivo potrebbe essere misurato in base alle sue caratteristiche chimico-fisiche, però in pratica tale lavoro differisce sensibilmente dagli schemi teorici, in quanto la composizione dei gas svi luppati dalla detonazione dipende da equilibri chimici legati alle condizioni termiche e bariche dell'insieme, le quali variano sensibilmente con le condizioni di dilatazione lasciate ai prodotti dell'esplosione. Di conseguenza il lavoro che un esplosivo può svolgere (quindi la sua potenza) viene determi nato con due prove pratiche, nelle quali è diverso il tipo di dilatazione dei prodotti della detonazione. Si tratta delle prove al blocco di piombo e al mortaio balistico, per le quali, come per altre, non avendo significato pratico i valori assoluti della prava, i risultati vengono riferiti a quelli di un esplosivo assunto come campione.
2.18 - Saggio del blocco di piombo (Trauzi) - Questa prova consiste nel misurare lo svasamento di una cavità praticata in un blocco di piombo quando si fa esplodere una certa quantità di esplosivo nella cavità.
Il blocco di piombo ha forma di un cilindro di diametro 200 mm, altezza 200 mm ; il foro assiale cilindrico di diametro 25 mm, profondo 125 mm, ha il volume di 61 cmc. Si fanno brillare nel foro cariche di 10 g di esplosivo innescato con un detonatore del n. 8 (cfr. n. 8.9) intasato con sabbia, e si ottengono vari aumenti della cavità iniziale. Si misurano questi volumi semplicemente versando nei fori acqua da una buret ta graduata, previa pulizia dei residui solidi: si chiamano
cifre di Trauzi, per i vari esplosivi, gli aumenti del volume iniziale, ossia i volumi misurati con l'acqua diminuiti del volume fisso iniziale di 61 cm 3 .
Le cifre di Trauzl sono da 540 a 570 cm 3 per la nitroglicerina; 500 - 540 cm 3 per la dinamite gomma, ecc.
Gli scarti dei valori per uno stesso esplosivo sono conseguenza delle condizioni di esperimento: qualità del piombo, del detonatore, dell'intasamento. La temperatura standard è di 15° C; ai risultati delle prove fatte a temperature differenti si applica la correzione di 0,25 cm 3 per ogni grado di differenza e per ogni 100 cm 3 di volume (si sottrae la correzione per temperature superiori a 15° C e viceversa).
Talvolta le cifre vengono riferite alla nitroglicerina, presa come 100, ed allora alla dinamite gomma corrisponde circa 90,
ecc.
La prova al blocco di piombo come ora descritta è quella detta
Trauzl internazionale 1903 perché è quella classica originale, accettata al V Congresso internazionale di chimica applicata di Berlino del 1903 su proposta dell'austriaco Trauzl. Successivamente, nel 1928,
Neubner ha mostrato essere vantaggioso prendere come unità la cavità prodotta al blocco di Trauzl da 10 g di dinamite standard, al 40% (nitroglicerina 40%, nitrato di sodio 44%, farina di legno 15%, inerti 1%) che è di circa 292 cm 3 (al netto dei 61 cm
3 iniziali), determinando il peso della carica degli altri esplosivi che dà la anzidetta cavità. Se la carica necessaria è C e si assegna alla dinamite standard potenza 100, la potenza P dell'esplosivo in esame sarà:
P = 100 * (10/C)
I valori di P si chiamano
coefficienti di utilizzazione pratica (C.U.P.).
La determinazione di C può essere laboriosa. Se allora una carica di peso C1 ha dato una cavità netta Vi anziché quella Vo = 292 cm
3 si calcola C supponendo che esista proporzionalità fra una carica e la cavità netta da essa prodotta. Si scrive quindi:
C 1 : V i = C : 292
Il metodo Neubner può essere modificato prendendo come unitaria la cavità prodotta da 15 g di dinamite standard al 40%,
che è di circa 500 cm
3; allora la formula da applicare diventa:
P= 100 * (15/C)
2.19
- La misura al blocco di Trauzl viene anche fatta secondo il
metodo francese, con il quale si determina per ogni esplosivo la carica C che produce uno svasamento uguale a quello di
15 g di acido picrico (cfr. n.
3.7) puro (melinite) che è di circa 485 cm 3 (al netto dei 61cm
3 iniziali). Questo sistema costituisce una misura dell'energia utilizzabile nell'esplosione, ammesso che a volumi uguali corrispondano uguali lavori e che l'energia sviluppata sia proporzionale al peso di esplosivo che è stato fatto brillare. In tal modo se di un dato esplosivo ne occorrono 18 g per produrre uno svasamento uguale a quello di 15 g di acido picrico, vuol dire che l'esplosivo in esame ha attitudine di lavoro al blocco di piombo di 15/18, ossia 0,84 rispetto all'acido picrico. Così viene eliminato l'effetto dei vari fattori che influiscono sulle prove eseguite con il metodo internazionale.
Gli esplosivi più potenti dell'acido picrico avranno indice superiore a uno. Infatti ad esempio la dinamite gomma ha indice 1,55.
Facendo le prove è difficile indovinare la quantità di esplosivo che dia uno svasamento S 2 perfettamente uguale a quello S1 dei 15g di acido picrico. Per non essere costretti a fare altre prove, se C2 è il peso della carica che ha dato lo svasamento S2 si calcola la carica C, che darebbe lo svasamento S, con la formula:
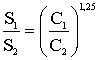
2.20 - Il mortaio balistico e il pendolo balistico - Il mortaio balistico (fig.2.4) è costituito da un blocco metallico, sospeso mediante aste a un asse orizzontale, che può oscillare solo in un piano verticale perpendicolare all'asse di sospensione. Nel blocco metallico viene inserita una piccola carica innescata, otturando poi il foro di ingresso con un cilindretto metallico.
Il peso del mortaio di tipo Hercules Powder (compreso l'albero di rotazione e il traliccio di alluminio, escluso il cilindretto ) è di 450,5
kg; il peso del cilindro è di 17,350 kg; il raggio di oscillazione sull'arco di graduazione è di 3,44 m.
L'esplosione della carica espelle il cilindro e, per reazione, il blocco metallico ruota di un certo angolo dalla parte della culatta. Il movimento del cilindro è accompagnato dallo spostamento di un cursore lungo un arco di cerchio sistemato in basso e che non torna indietro con la culatta, per cui segna il massimo angolo raggiunto, con l'approssimazione di un primo sessagesimale.
Si assume come valore 100 l'angolo a o
di cui ruota il mortaio con una carica (di solito 10 g) di dinamite gomma (media di 10 determinazioni), angolo che oscilla fra 20° e 25° (gli corrisponde uno spostamento del blocco metallico lungo l'arco da 1 a 1,30 m). Successivamente (pure come media di 10 determinazioni) si determina l'angolo a
che corrisponde allo stesso peso di esplosivo in prova.
L'innalzamento h o del centro del mortaio in corrispondenza all'angolo ao , se l è la sua distanza dal centro di rotazione, risulta uguale a:
ho = 1(1 -cos ao )
Il valore corrispondente per l'esplosivo in prova è:
h=1(1-cos a )
Allora la
potenza al mortaio balistico (P.M.B.), detta anche
power o weight strength MS.), o anche semplicemente
strength (in italiano
forza), per l'esplosivo in prova è data da:
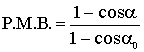
I valori della forza vengono anche chiamati
coefficienti di utilizzazione pratica al mortaio balistico (C.U.P.M.B.).
Bisogna però tener presente che, per uno stesso esplosivo, la dinamica di ottenimento del foro nel blocco Trauzl è diversa da quella che produce la oscillazione del blocco nel mortaio balistico; ad esempio la densità e la granulometria degli ingredienti possono influire diversamente nelle due apparecchiature. Da questo discende che i valori C.U.P. e quelli W.S. non possono essere confrontati senza procedere a una opportuna interpretazione.
2.21 - Un'apparecchiatura analoga per la stessa prova è quella del
pendolo balistico (fig. 2.5)
nella quale la carica (abbastanza forte, di solito 250 g) esplode in un piccolo mortaio. mobile su rotaia che si porta a contatto con un cilindro di acciaio, forato fino a una certa profondità, molto pesante, sospeso come un pendolo. Per effetto dell'esplosione un cilindro di acciaio, messo a chiusura della carica, esce dal mortaio e (mentre questo rincula lungo la rotaia) penetra con violenza nel foro del pendolo, facendolo girare di un certo angolo dalla parte opposta. I valori relativi si calcolano come nel caso del mortaio balistico.
Saggi per la misura della dirompenza (Hess, Kast e incavo della piastra) -
La determinazione della dirompenza viene fatta normalmente con due prove analoghe, classiche, o con una moderna.
2.22 - Con la prova di
Hess si
misura lo schiacciamento di due cilindri di piombo sopra cui si fa esplodere una carica dell'esplosivo da provare. I due cilindri (di diametro 40 mm, alti 30 mm) vengono appoggiati sovrapposti su una piastra di acciaio e ricoperti da un disco di acciaio sopra il quale si fa esplodere una piccola carica di 50 g contenuta in un cappellotto di alluminio.
Al momento dell'esplosione il cilindro superiore assorbe la maggior parte dell'azione d'urto mentre quello inferiore assorbe prevalentemente la azione di spinta. Si ha quindi un maggiore schiacciamento del cilindro superiore per esplosivi veloci; per gli esplosivi più lenti lo schiacciamento dei due cilindri è circa lo stesso.
Il saggio di Hess può essere modificato con un solo cilindro (fig. 2.7).
2.23
- La prova di
Kast consiste nel misurare lo schiacciamento prodotto su un cilindretto
(crusher) di rame (di diametro
7 mm,
altezza 10,5 mm) dalla detonazione di una carica di esplosivo; la carica è libera nell'aria, appoggiata sul
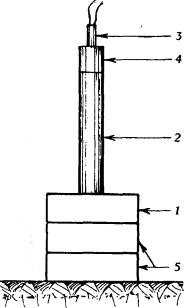
Fig. 2.8 (a destra) - Schema di attrezzatura per la prova dell'incavo della piastra
cilindro (posto sempre con l'asse verticale) che schiaccia il crusher. La carica è anche di 100 g; i valori sono riferiti a quelli della dinamite gomma o dell'acido picrico.
2.24 -
Le due prove precedenti sono piuttosto antiche (quella di Hess risale a poco dopo il 1870
) e i risultati che con esse si ottengono non sono né perfetti né omogenei con la prova del blocco di Trauzl. Si tende perciò oggi a sostituire queste prove con quella detta
prova dell'incavo della piastra (plate-denting test) messa a punto dall'Explosive Research Laboratory di Bruceton (Pennsylvania). La prova viene effettuata appoggiando (fig. 2.8) su una piastra di acciaio 1) di durezza stabilita (avente spessore di 50 mm e lato di 152 mm) in posizione verticale una cartuccia 2) dell'esplosivo da provare (diametro della cartuccia 41,2 mm, altezza 203 mm). La cartuccia è innescata da un detonatore elettrico 3) inserito in una piccola carica di esplosivo potente 4) che viene appoggiata sulla sommità della cartuccia. La piastra 1) di solito poggia su una o due piastre 5) di rinforzo. L'esplosione della cartuccia provoca un incavo nella piastra (per gli esplosivi da mina si tratta in genere di una frazione di millimetro); le profondità ottenute vengono normalmente riferite a quella provocata da una cartuccia di tritolo.
Densità
2.25 - Bisogna distinguere:
1) la
densità assoluta, o reale, o peso specifico, che rappresenta il peso di un certo volume nel quale la sostanza è contenuta senza interspazi (la si chiama per questo anche
densità di cristallo);
2) la
densità gravimetrica, o apparente, che è il rapporto fra il peso di un certo volume di esplosivo nelle condizioni normali in cui è fornito (ossia comprese le inclusioni gassose) e il volume che esso occupa. Questa densità è minore di quella assoluta: la differenza è piccola per gli esplosivi plastici, maggiore per quelli pulverulenti;
3) la densità di carica, ossia il peso di esplosivo contenuto nell'unità di spazio del foro da mina (o della camera) in cui avverrà l'esplosione.
Tutte queste densità vengono espresse in chilogrammi per litro.
Aumentando la suddivisione dei grani e la pressione applicata aumenta la densità apparente ma essa non può mai raggiungere la densità assoluta.
Al n. 2.12 si è accennato che con il crescere della densità di carica aumenta in genere la velocità di detonazione. Si ricorderà anche che l'onda esplosiva si propaga attraverso l'esplosivo stesso come un'onda sonora, ma che la velocità di trasmissione è modificata dall'alta pressione generata. Inoltre aumentando la densità, quindi riducendosi la compressibilità, aumenta il modulo di elasticità e diminuisce la sensibilità (questa diminuzione di sensibilità viene attribuita al fatto che l'energia data a una particella viene dissipata rapidamente nel mezzo più denso e più rigido con la conseguenza che per ottenere la detonazione bisogna imprimere all'esplosivo un impulso più potente); se si potesse raggiungere la densità di cristallo non si avrebbe più detonazione.
Naturalmente partendo da densità di carica piccole la velocità di esplosione aumenta con l'aumentare della densità, però fino a un certo limite oltre il quale la velocità diminuisce fino ad annullarsi. La densità per cui la velocità è massima si chiama
densità di carica limite pratica ed è quella che è opportuno adottare nelle mine per avere il massimo rendimento.
Per alcuni esplosivi la densità pratica di caricamento è inferiore alla densità limite, (il tritolo ha velocità di detonazione 4200 m/s a densità 0,8 e velocità 7000 m/s a densità 1,6, con andamento lineare per i valori intermedi), per altri la densità di carica limite può essere raggiunta facilmente (per una cheddite il diagramma è risultato quello di fig. 2.9).

Fig. 2.9 - Relazione fra la densità di carica e la velocità di detonazione per un esplosivo di tipo cheddite
Questo comportamento degli esplosivi spiega perché qualche volta mine con carica lunga non detonano completamente: l'onda di esplosione che parte dall'estremità della carica ove c'è l'innesco comprime l'esplosivo della parte più lontana e si può lì raggiungere e superare la densità limite, per cui resta una parte di carica inesplosa.
La pressione contro le pareti del foro da mina aumenta con il crescere della densità di carica (pur di restare, ora si aggiunge, sotto la densità limite).
Ecco il rapporto, secondo Taffanel e Dautriche, per la dinamite gelatina:


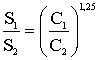

 Fig. 2.9 - Relazione fra la densità di carica e la velocità di detonazione per un esplosivo di tipo cheddite
Fig. 2.9 - Relazione fra la densità di carica e la velocità di detonazione per un esplosivo di tipo cheddite ![]()
![]()