Disegnare una traiettoria

Esiste un metodo semplicissimo per tracciare la traiettoria di un proiettile sulla base di pochissimi dati: l'angolo di proiezione, la gittata e il tempo di volo (oppure l'ordinata al vertice della traiettoria). La curva così disegnata differisce dalla curva reale in modo non apprezzabile nella scala grafica abitualmente usata.
Il metodo è stato proposto dal balistico tedesco Schmidt e parte dall'idea di assimilare la traiettoria ad una parabola asimmetrica e con asse inclinato, quale si avrebbe nel vuoto se il proiettile fosse assoggettato ad una forza costante agente in direzione dell'asse della parabola e quindi trasversalmente. Questa forza può essere immaginata come la risultante della forza di gravità effettiva e di un'altra forza diretta all'indietro e che rappresenta la resistenza dell'aria; sebbene questa forza, a differenza della resistenza dell'aria, sia immaginata come costante in grandezza e direzione, essa ben ne simula il risultato globale in quanto dedotta dal dato effettivo della gittata e della ordinata al vertice della traiettoria (la quale ordinata si ricava anche con buona approssimazione dal tempo totale di volo secondo la formula di Haupt:

yv = 1,25 T² Per il tracciamento grafico della curva, lo Schmidt fa uso della proprietà della parabola secondo cui la linea che congiunge la metà di due tratti di tangente, misurati dal punto di contatto al punto di incontro, è a sua volta una tangente della curva.
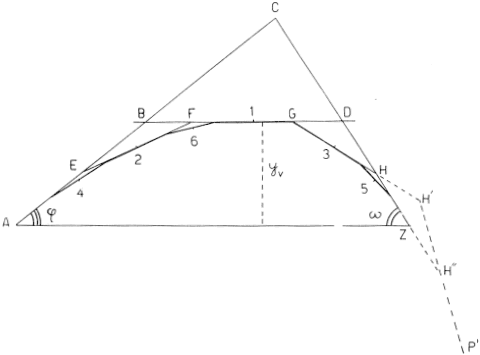
Si tracci in scala la linea AZ (fig.1) corrispondente alla gittata X del proiettile; in A si tracci l'angolo di proiezione j . Alla distanza yv , già nota o ricavata con la formula di Haupt, si tracci BD parallela ad AZ, si raddoppi quindi il tratto AB, così che sia AB = BC; la congiungente CZ sarà la tangente all'angolo di caduta w che potrà essere misurato o calcolato trigonometricamente. La linea BD congiungente i punti intermedi delle tangenti AC e CZ, sarà a sua volta una tangente; il punto di contatto si otterrà dividendo BD a metà e il punto -1- così ottenuto sarà il vertice della traiettoria.
Si dividano ora a metà i tratti A-B e B-1 del ramo ascendente e i tratti D-Z e D-1 del ramo discendente, ottenendo i punti E-F-G-H-; si congiunga E con F e G con H e si dividano i segmenti così ottenuti a metà; i punti -2- e -3- così ottenuti saranno altri due punti di contatto di tangenti e quindi punti della parabola ricercata. Si dividano a metà i tratti 2-E ed A-E, e si congiungano i punti trovati; la metà della congiungente sarà un ulteriore punto della parabola. Allo stesso modo si procederà per il ramo discendente fino ad avere un numero sufficiente di punti (in genere 5 o 7) che, congiunti fra di loro, forniranno la traiettoria ricercata. Questa, per chiarezza, non è tracciata in figura.
Il disegno risulterà facilitato se si userà carta millimetrata, osservando che i punti E ed H e quelli successivi ricavandi sui tratti BA e DZ sono pari a 1/2, 1/4, 1/8 della altezza Yv.
Nel caso si volesse proseguire la curva al di sotto della linea di orizzonte, come può richiedersi in alcuni casi, è agevole proseguire la costruzione considerando che, se si prolungano verso l'esterno i semi-segmenti di tangente sopra ricavati (ad esempio 3H) di una quantità eguale e si congiunge il punto H' trovato con il prolungamento ZH''=HZ, il punto P dato da H'H"=H''P sarà anch'esso un punto della curva.
Il sistema dello Schmidt consente di raggiungere una ancor maggiore precisione se è noto anche l'angolo di caduta: è chiaro che in tal caso i due rami della traiettoria verranno costruiti separatamente tracciando la tangente CZ secondo l'angolo effettivo.