Il cofficiente di forma - i -

Il coefficiente aerodinamico (Cx) di un proiettile ne descrive esattamente il comportamento aerodinamico alle varie velocità e in una data atmosfera, tenendo conto di tutti i fattori: peso e volume del proiettile, forma della punta, del corpo e della coda, tipo di superficie, atmosfera.
Esso può essere calcolato mediante calcoli aerodinamici piuttosto complessi.
Il coefficiente balistico (Cb) di un proiettile, come visto alla relativa voce, è ricavato dal calibro e peso di un determinato proiettile, secondo una formula valida esclusivamente per una certe legge di resistenza (il che non esclude che leggi diverse adottino la medesima formula) che si basa su di un proiettile ideale. Se il proiettile concreto in relazione a cui si vuole eseguire un calcolo ha la stessa forma, è sufficiente variare peso e calibro per potergli applicare la legge di resistenza usata; se invece il proiettile ha una forma diversa, occorre introdurre un valore correttivo che tenga conto della diversa penetrazione aerodinamica.
Questo valore correttivo viene chiamato fattore di forma "i" (talvolta anche coefficiente di forma) che, ovviamente, per il proiettile ideale ha il valore di 1.
Un'immagine renderà più chiaro il concetto.

Coeff. Cx di alcuni proiettili ideali o reali: 1 - Proiettile cilindrico cal. 10 cm. 2 - Palla sferica. 3 - Proiettile ideale di Majewsky. 4 - Proiettile ideale di Eberhard. 5 - Proiettile ideale di Siacci. 6 - Proiettile ideale legge sovietica 1943. 7 - Proiettile Flak cal. 8,8 cm.
Il fattore di forma di una palla sferica, ad esempio, sarà dato da quel coefficiente che ci consente, moltiplicando i valori della curva 3 della legge di Mayewsky, di ottenere i valori rappresentati nella curva 2. Come si vede agevolmente dalla figura, questo valore varia molto a seconda della velocità ed ha un senso solo se applicato a brevi tratti di traiettoria. Talvolta è costante per velocità supersoniche (si veda come decorrano pressoché parallele le curve 2, 4 e 6 oltre i 500 ms), ma è soggetto a variazioni notevoli in prossimità del muro del suono.
Siccome però i balistici in qualche modo i loro calcoli li dovevano fare, hanno convenuto di usare un fattore di forma globale che rappresentasse, per ogni proiettile, la miglior approssimazione possibile.
Conoscendo i dati balistici di un proiettile (peso, calibro, velocità iniziale e velocità finale su di una data tratta) è possibile risalire al suo coefficiente di forma, relativo ad una data legge di resistenza, con le formule indicate alle voci coefficiente balistico e tavole di ritardazione.
Se non si dispone di questi dati si deve ricorrere ad altri mezzi. Il più pratico è fornito dalla tavola di Burgless-Coxe che ha il seguente aspetto

Siccome essa deve essere usata a grandeza naturale, l'immagine ingrandita può essere scaricata cliccando qui.
Immagine in scala di Burgless-Coxe
La figura serve per individuare, sovrapponendolo ad essa, il raggio in calibri dell'ogiva del proiettile che si studia. Individuato il raggio, si entra con esso nella seguente tabella

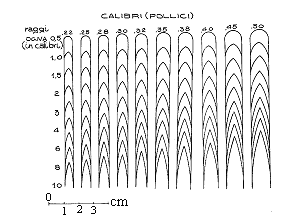
                                           Punta    Punta piatta o cava il cui
                                          Normale  diametro è espresso in calibri
                                                     0,1   0,2   0,3   0,4   0,5
Tozzo, cilindrico                           2,30
  "   parte curva di 0,9 cal.               1,85
  "     "     "      0,8  "                 1,50
  "     "     "      0,7  "                 1,30
  "     "     "      0,6  "                 1,10
Ogiva con raggio  di 0,5  "                 1,40
  "           "      1    "                 1,10     1,15  1,20  1,25  1,30  1,40
  "           "      1,5  "                 0,95     1,00  1,10  1,15  1,25  1,35
  "           "      2    "                 0,85     0,90  0,95  1,00  1,10  1,25
  "           "      3    "  vel. > 600 ms  0,70     0,75  0,80  0,90  1,00  1,10
  "           "      3    "  vel. < 600 ms  0,75     0,80  0,85  0,95  1,05  1,15
  "           "      4    "  vel. > 600 ms  0,60     0,65  0,70  0,75  0,85  1,00
  "           "      4    "  vel. < 600 ms  0,70     0,75  0,80  0,85  0,95  1,10
  "           "      6    "  vel. > 600 ms  0,55     0,60  0,65  0,70  0,80  0,95
  "           "      6    "  vel. < 600 ms  0,65     0,70  0,80  0,85  0,95  1,10
  "           "      8    "  vel. > 600 ms  0,49     0,55  0,60  0,65  0,75  0,90
  "           "      8    "  vel. < 600 ms  0,60     0,65  0,70  0,75  0,85  1,00
  "           "      10   "  vel. > 600 ms  0,44     0,50  0,55  0,60  0,70  0,85
  "           "      10   "  vel. < 600 ms  0,55     0,60  0,66  0,70  0,80  0,95
palla sferica                vel. < 300 ms  2,00
  "      "                   vel. > 300 ms  1,70
  "      "                   vel. > 400 ms  1,40

I concetti di raggio di curvatura e di appiattimento in calibri sono chiariti nell'immagine che segue L'uso della tabella è questo: individuato più o meno il raggio di curvatura dell'ogiva si entra nella tabella in cui nella prima colonna (punta normale) sono indicati i valori per proiettili a punta tondeggiante o appuntita. Se invece il proiettile è a punta appiattita o cava, il valore andrà ricavato dalle restanti colonne.
Particolari conformazioni del proiettile comportano ulteriori diminuzioni del fattore di forma. Se il corpo del proiettile (parte tra la coda rastremata e l'ogiva) è più corto di 5 calibri il fattore di forma va così diminuito
Corpo = 4 calibri - 0,01
Corpo = 3 calibri - 0,03
Corpo = 2 calibri - 0,04
Corpo = 1 calibri - 0,05
Il cono di base (rastrematura) con un angolo standard di 15° comporta una diminuzione del coeff. di forma di -0,08; la presenza di mantellatura sporgente (Scharfrand) comporta un aumento di +0,15; la presenza di punta di piombo fuori della mantellatura e lunga più di 0,3 calibri un aumento di +0,06.
Vediamo ora un esempio. Sia il proiettile 8x57 JS HMB Norma a base rastremata e punta di piombo, sopra raffigurato, con ogiva pari a 32 mm. e quindi 4 calibri.
Si avrà in relazione ad una velocità iniziale di 755 ms:
-valore della tabella                                            0,60
-arrotondamento della punta pari a 0,5 calibri    +0,40
-cono di base                                                   -0,08
-punta di piombo                                             +0,06
e quindi un fattore di forma pari a 0,98

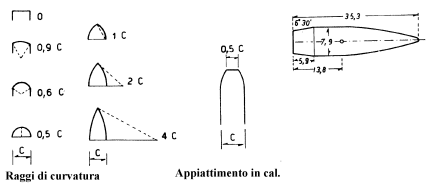
Il fattore di forma può essere dedotto dalla perdita di velocità del proiettile su di una certa tratta, se si possiedono dei dati esatti, come esposti in molte tabelle dei produttori. Si utilizzano i dati per la tratta da 200 a 300 metri e il fattore di forma i sarà dato da:

in cui
P = Peso grammi/1000
DV = Perdita di velocità da 200 a 300 metri
T = Tempo di volo sulla tratta da 200 a 300 metri
R = Calibro in mm /2000
I valori di m ed n sono quelli usati nella funzione f(v) secondo Majevsky (vedi il capitolo Coefficiente balistico), utilizzando come velocità quella media tra velocità iniziale e velocità finale sul tratto.
 

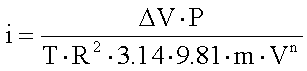
Velocità	m	n
0   - 240	0.0140	2
240 - 295	0.05834	3
295 - 375	0.06709	5
375 - 419	0.09404	3
419 - 550	0.03940	2
550 - 800	0.2616	1.7
800 - 1000	0.7130	1.55

Chi volesse un programmino per calcolare il fattore i con il metodo esposto, lo scarichi cliccando qui .
Vi è una formula specifica per i proiettili appuntiti di fanteria e che non può essere adottata per altri proiettili:

La formula dà le variazioni di i in funzione della velocità.
La ritardazione

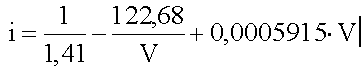
Noti il coefficiente balistico e il coefficiente di forma, sarà facile calcolare la ritardazione del proiettile ad una data velocità; questa è l'accelerazione negativa subita dal proiettile per effetto della resistenza dell'aria.
La resistenza dell'aria in kg si calcola moltiplicando il coefficiente balistico per il valore di f(v) ricavato da una delle varie leggi di resistenza (vedi la pagina sul coeff. bal.) secondo la formula

dove C è il calibro in metri, v la velocità in ms e d/do indica il rapporto fra la densità dell'aria e la densità standard pari a kg 1,225.

La ritardazione si ottiene dividendo la Resistenza per la Massa; questa è data dal Peso in kg diviso per la gravità e, in conclusione la ritardazione Rit. sarà data dalla formula

Se invece di far ricorso ai valori di f(v) si calcola sulla base del coefficiente aerodinamico Cx, la ritardazione sarà data da

in cui A è la sezione del proiettile in centimetri quadrati, delta la densità dell'aria in kg per metro cubo, v la velocità in Mach.

Per chi volesse controllare il risultato dei propri calcoli, vediamo un esempio pratico.
Si voglia conoscere la ritardazione di un proiettile cal 8x57 militare alla velocità di 750 ms. Il peso è 12 gr. Il raggio di ogiva è di 10 calibri e il fattore di forma è i=0,445.
Applicando le funzioni di Sängewald si ha che f(750)=2

Applicando invece il valore di Cx pari a 0,30 per la velocità di 2,2 Mach, si ha

In entrambi i casi la ritardazione sarà data da

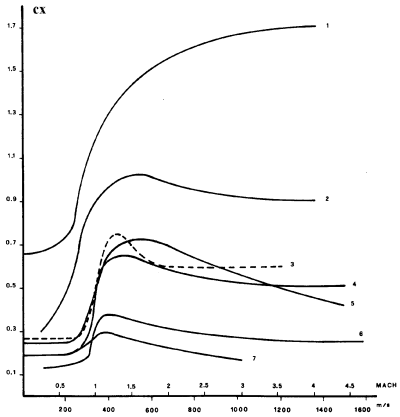
Riporto qui sotto una pratica tabella in cui sono indicati i valori di Cx per i proiettili ideali di Eberhard (Sängewald) e Mayewsky. Ovviamente i valori tabulati per le rispettive funzioni sono più esatti.

Mach   ms     cx Sän. Cx Majewsky
0,1    34     0,194    0,228
0,2    68     0 194    0,228
0,3    102    0,194    0,228
0,4    136    0,194    0,228
0,5    170    0,194    0,228
0,6    204    0,195    0,228
0,7    238    0,198    0,228
0,8    272    0,216    0,259
0,9    306    0,268    0,313
1      340    0,463    0,430
1,1    374    0,598    0,573
1,2    408    0,632    0,626
1,3    442    0,647    0,643
1,4    476    0,652    0,643
1,5    510    0,651    0,643
1,6    544    0,644    0,643
1,7    578    0,635    0,633
1,8    612    0,624    0,623
1,9    646    0,611    0,613
2      680    0,602    0,603
2,1    714    0,592    0,594
2,2    748    0,583    0,586
2,3    782             0,578
2,4    810             0,571
2,5    850             0,559
2,6    884             0,549
2,7    918             0,540
2,8    952             0,531
2,9    980             0,521