
 |
| back |
La balistica è quel ramo della fisica meccanica che studia il moto dei proiettili. Appare opportuno richiamarne, per completezza di trattazione, la terminologia ed i principi fondamentali di più diretto impiego.
I corpi hanno la proprietà della mobilità e
della inerzia.
Dicesi mobilità la facoltà dei corpi di poter occupare
successivamente diverse posizioni nello spazio. Un corpo può trovarsi
in movimento oppure in stato di quiete o riposo.
Dicesi inerzia la proprietà per la quale un corpo non
può da solo modificare il suo stato di quiete o di moto.
Secondo il principio d'inerzia "lo stato di quiete o di movimento
di un corpo abbandonato a se stesso non può essere modificato che da
una causa esterna agente sul corpo".
Forza è appunto la causa esterna capace di produrre o modificare
un moto, cioè di vincere l'inerzia.
Gravità è la forza che fa cadere un corpo solido quando
è liberamente abbandonato a se stesso e si manifesta come peso sopra
un appoggio che impedisce al corpo di cadere. La forza di gravità agisce
su tutte le singole molecole che costituiscono un corpo. Il punto invariabile
di un corpo, per cui passa la risultante di tutte le azioni eguali e parallele
che la gravità esercita sulle diverse molecole è detto centro
di gravità.
Il movimento di un corpo è caratterizzato dalla
traiettoria e dalle leggi del moto.
Traiettoria è la linea continua costituita dalle diverse posizioni
occupate dal centro di gravità del corpo in tempi successivi (può
essere rettilinea, curvilinea, ecc.).
Direzione del moto, in un punto qualunque di una traiettoria curvilinea,
è la direzione della tangente alla traiettoria in quel punto.
Legge del moto è la relazione che esiste tra gli spazi percorsi
dal corpo ed i tempi impiegati a percorrerli.
Il moto può essere uniforme o vario.
Si dice che un corpo possiede moto uniforme quando in tempi eguali
e successivi, comunque piccoli, percorre spazi eguali e nella stessa direzione;
vale a dire che gli spazi percorsi dal mobile sono proporzionali ai tempi
impiegati a percorrerli.
Dicesi velocità di un moto uniforme lo spazio percorso dal mobile nell'unità
di tempo.
La formula del moto uniforme è
S = Vt da cui V =S/t e t = S/V
Nella rappresentazione grafica con assi cartesiani il moto
uniforme è rappresentato da una linea retta.
Ogni moto non uniforme è "vario". In esso il rapporto spazio/tempo,
cioè la velocità, varia nel periodo considerato.
Poiché la velocità varia da un istante all'altro, non potrà
più parlarsi di velocità in genere, ma di velocità istantanea
(vale a dire la velocità del mobile in un determinato istante, ovvero
velocità che il mobile avrebbe in quel momento se cessasse ogni variazione
di rapporto spazio temporale ed il moto diventasse uniforme), e velocità
media in un dato intervallo di tempo, (vale a dire la velocità riferita
al moto uniforme, con il quale il mobile percorrerebbe lo stesso spazio durante
lo stesso tempo).
Il moto vario è accelerato se la sua velocità
cresce col tempo, ritardato se decresce.
Se la velocità cresce o decresce proporzionalmente al tempo, il moto
dicesi uniformemente accelerato o ritardato.
Accelerazione dicesi la misura costante di cui la velocità cresce
o decresce durante ogni unità di tempo. Essa è positiva nel
moto uniformemente accelerato, negativa nel moto uniformemente ritardato.
Indicando con "a" l'accelerazione e con "Vo " la velocità
iniziale, la velocità finale "V" sarà data da
V = Vo + at per il m.u. accelerato
V = Vo - at per il m.u. ritardato
Se il corpo parte dallo stato di quiete, si ha Vo = 0 e quindi
V = at
Graficamente, la curva delle velocità nel moto uniformemente vario
è una linea retta. La curva degli spazi è una parabola.
Le formule che descrivono il moto uniforme vario sono riportate nella tavola
che segue.
MOTO UNIFORMEMENTE ACCELERATO O RITARDATO
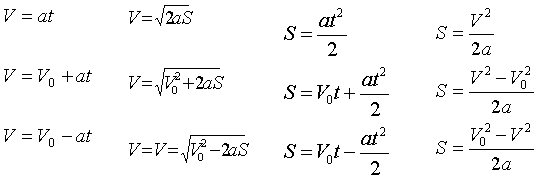
NOTA: Nella prima riga sono riportate le formule per il moto accelerato senza
velicità iniziale
Nella seconda riga quelle con velocità iniziale.
Nella terza le formule per il moto uniformemente ritardato.
Se in luogo dell'accelerazione -a- si pone la gravità -g- e in luogo
di -S- si pone l'altezza di caduta -H-, le formule risolvono problemi relativi
alla caduta dei gravi (m. u. accelerato) o al lancio dei gravi verso l'alto
(m. u. ritardato). Le relazioni tra le forze ed i movimenti che esse causano
sono studiate dalla dinamica.
Leggi fondamentali della dinamica sono
LEGGE DI INERZIA (Keplero): un corpo in riposo non può mettersi da
sé in movimento. Un corpo materiale in movimento non può da
sé modificare la misura né la direzione della propria velocità.
Da un diverso punto di vista si può dire che un corpo che non subisce
influenze esterne non può essere che in quiete o animato da moto rettilineo
uniforme.
UGUAGLIANZA DELL'AZIONE E DELLA REAZIONE (NEWTON): tutte le volte che un corpo
agisce su di un altro corpo rigido, questi reagisce sul primo con una forza
uguale di senso contrario.
MOVIMENTI RELATIVI (Galileo): L'effetto di una forza su di un corpo è
indipendentedal movimento anteriormente posseduto dal corpo stesso. Una forza
costante che agisce su di un corpo può dar luogo a tre diversi tipi
di movimento:
a) agendo su di un corpo libero in quiete, gli imprime un moto rettilineo
uniformemente accelerato;
b) agendo su di un corpo animato di velocità iniziale e nella stessa
direzione, gli imprime un movimento rettilineo uniformemente accelerato;
c) agendo su di un corpo animato da una velocità iniziale avente diversa
direzione, gli imprime un moto parabolico.
La gravità è una forza che può ritenersi
costante: perciò un corpo nel vuoto cadrà con moto uniformemente
accelerato. I problemi relativi alla caduta dei corpi nel vuoto saranno quindi
risolvibili con le formule della tabella 1 sopra riportate in cui l'accelerazione
"a" sarà rappresentata dalla gravità "g".
La gravità è misurata dal doppio dello spazio percorso dal corpo
durante il primo secondo di caduta ed il suo valore medio sul livello del
mare è di m. 9,81 al secondo per secondo.
I valori effettivi variano da 9,781 all'equatore a 9,831 ai poli.
Dalla formula V = Vo - gt si ricava che un corpo lanciato in alto si arresta
dopo un tempo t = Vo/g
Inserendo questo valore di t nella formula
H = Vot – (gt²/2)
si ricava che il corpo si arresterà dopo aver percorso lo spazio
H = Vo²/2g
Esempi: Un sasso raggiunge il fondo di un pozzo dopo 5". Quanto
è profondo il pozzo, trascurando la resistenza dell'aria?
H= 9,81 x 5²/2 = 122,62 m
Un sasso è lanciato in alto con velocità iniziale di 49 m/sec.
Quale altezza avrà raggiunto dopo 3" e quale sarà l'altezza
massima raggiunta?
H= 9,81 x 3²/2 = 102,85 m
Il tempo in cui si arresterà
t= 49/9,81 = 5"
L’altezza massima sarà 49²/ (2 x 9,91) = 122,6 m
Quando più forze agiscono simultaneamente su di un
corpo, ognuna di esse opera effetti indipendenti dalle altre. Se una delle
forze F è il peso P del corpo, l'accelerazione corrispondente sarà
quella "g" dovuta alla gravità sicché
F = Pa/g
vale a dire che il valore della forza è misurato dal peso del corpo
moltiplicato per il rapporto fra accelerazione "a" dovuta alla forza e quella
"g" dovuta alla gravità.
Massa è il rapporto fra il peso del corpo e
l'accelerazione di gravità
M =P/G da cui P= Mg
o, in generale,
F = Ma
Il prodotto Ma rappresenta la misura dinamica di una forza: l'intensità
di una forza è uguale al prodotto della massa del corpo a cui è
applicata per l'accelerazione del movimento che essa produce.
Esempi: Sopra un corpo che pesa 300 Kg. agisce una forza costante
che produce l'accelerazione di 3 m/sec². Determinare F
F = 300 x 3 / 9,81 = 91,74 kg
-Che accelerazione produrrà su di un corpo pesante 500 kg. una forza
costante di 50 kg?
a = 50 x 9,81 / 500 = 0,981 m/sec
-Che forza ha agito su di un corpo pesante kg.2000 per farlo passare in 15"
dalla velocità di 10 m/sec alla velocità di 115 m/sec. ?
V= Vo + at; 115 = 10 + 15a; a = 7 m/sec
F = 200 x 7 / 9,81 = 1427 kg
L'unità di massa è quella di un corpo al quale
la forza di un kg. imprime l'accelerazione di 1 m/sec².
L'unità di forza è quella forza che agendo sull'unità
di massa le imprime l'accelerazione di 1 m/sec² .
La "quantità di moto" di un corpo in movimento è il prodotto
MV della sua massa per la velocità che esso possiede nell'istante considerato.
Da ciò il principio importantissimo che le velocità impresse
da una stessa forza a corpi di massa diversa sono inversamente proporzionali
alle masse dei corpi ed ancora, che quando una determinata forza agisce per
lo stesso tempo su corpi di massa diversa, la quantità di moto è
la stessa; in pratica quello che si guadagna in massa posta in movimento,
si perde in velocità e viceversa.
Una forza quindi imprime a due corpi di peso diverso velocità
inversamente proporzionali ai rispettivi pesi:
V : V’ = P’ : P
Una forza imprime a due corpi di peso diverso accelerazioni
inversamente proporzionali alle rispettive masse.
M : M’ = a’ : a
L'impulso è il prodotto di una forza per il
tempo durante il quale essa agisce. L'impulso di una forza costante agente
su di un corpo che parte dalla quiete è eguale alla quantità
di moto
Ft = MV
Non esistono forze istantanee.
Forza di inerzia è quella forza contraria alla forza F e capace di equilibrarla.
Il lavoro di una forza costante applicata ad un corpo è
dato dal prodotto dell'intensità della forza agente nel senso del moto
per lo spazio percorso dal corpo
L = FS
Unitàdilavoro è il chilogrammetro(kgm )che corrisponde
al sollevamento del peso di un kg. all'altezza di un metro. Questo valore
è indipendente dalla durata, cioè dal tempo impiegato a compiere
il lavoro.
Nel nuovo sistema di unità di misura si usa il Joule; 1 kgm = 9,81
J
Forza viva: se un corpo è dotato di moto
di traslazione, dicesi forza viva il prodotto della sua massa per il quadrato
della sua velocità M.V².
Affinché un corpo di massa M dalla quiete venga messo in moto con una
data velocità V, occorrerà spendere, un lavoro eguale alla metà
della forza viva
L = MV²/2
detto anche energia cinetica.
Se il corpo già possedeva una velocità iniziale
V si avrà
L = M(V² - Vo²)/2
Inversamente, un corpo in movimento che si ferma è capace di produrre
un lavoro. eguale a quello speso per metterlo in movimento e per fargli acquistare
la velocità prima posseduta.
URTO DEI CORPI
Teorema di Carnot: nell'urto tra corpi anelastici o molli si verifica sempre
una cessione di forza viva e perciò di lavoro; nello urto tra corpi
perfettamente elastici non vi è perdita di forza viva e non si perde
quindi lavoro. Nell'urto tra due corpi M e M' molli che si muovono nella stessa
direzione con velocità V e V', la velocità comune Vo dopo l'impatto
sarà
Vo = (MC+ M’V’)/(M+M’)
Se i corpi si muovono in senso contrario si avrà
Vo = (MV – MV’)/(M+M’)
e quindi in generale
Vo = (MV± M’V’)/(M+M’) = (PV±
P’V’)/(P+P’)
Se uno dei due corpi è fermo e quindi V' = 0 si avrà
Vo = MV/(M+M’)
Nell'urto diretto fra corpi elastici, in pratica, vi è uno scambio
di velocità. La perdita di velocità subita dal corpo urtante
è doppia di quella che avrebbe subito se il corpo fosse stato anelastico;
la velocità acquistata dal corpo urtato è doppia di quella che
avrebbe acquistato se fosse stato anelastico. Dati quindi i due corpi elastíci
A e B che si muovono stessa direzione con velocità V e V' , le velocità
Va e Vb dopo l'urto, e con Vo la velocità che avrebbero acquistato
se anelastici, sarà
Va = 2V0 – V e Vb = 2V0 – V’
Se le masse dei due corpi fossero eguali, si avrebbe un esatto scambio di velocità; se il corpo urtato fosse fermo e di egual massa di quello che lo investe, si arresterebbe, mentre quello urtato si muoverebbe con la velocità del primo.
Conversione di misure anglosassoni
moltiplicando per si ottiene cm 0,3937 pollici pollici 2,540 cm metri 3,2808 piedi piedi 0,3048 m metri 1,0936 yarde yarde 0,914 m metri 39,37 pollici km 0,6214 miglia miglio 1,6093 km miglio mar. 1,852 km m/s 3,2808 ft/s ft/s 0,3048 m/s m/s 3,60 km/h km/h 0,2778 m/s ft/s 0,6818 m.p.h.(miles per hour) m.p.h. 0,447 m/s cm² 0,1550 sq.in. sq.in. 6,4516 cm² m² 10,764 sq. ft. s q. ft. 0,0929 m² cm cub 0,061024 cu.in. cu.in. 16,387 cm cub dcm cub 0,0353 cu.ft. cu.ft. 28,317 dcm cub metro cub 35,315 cu.ft. 1 (litro) 1,76 pinte grammo 15,432 grs (grani) gr.(grano) 0,0648 grammo grammo 0,564 drs (dracme) drs 1,772 grammo grammo 0,0353 oz (once) oz 28,349 grammo kg 2,2046 lbs (libbre) lb 0,45359 kg t(tonnellate) 0,9842 ton ton. 1,016 t kgm. 7,233 ft.lb. ftlb. 0,1383 kgm at (kg/cm²) 14,227 psi(pounds/square inch) psi 0,0703 at
| Sitemap: in Italiano | auf Deutsch | in English | |
| http://www.earmi.it - Enciclopedia delle armi © 1997 - 2003 |