search

	Home > Balistica > Sottomenu > Documento	back

Errori nel tiro

Errore di partenza
Nei calcoli eseguiti finora abbiamo sempre supposto che l'angolo di proiezione coincidesse con l'angolo di tiro, che cioè la posizione della bocca dell'arma e il prolungamento del suo asse non si spostassero durante lo sparo.
In effetti i due angoli non coincidono mai, ma divergono di un piccolo angolo detto angolo "di rilevamento". Quindi l'angolo di proiezione j sarà eguale all'angolo di tiro, più o meno un certo angolo r
L'angolo di rilevamento di cui si tiene conto solitamente è quello cadente nel piano verticale, ma al momento dello sparo si verificano anche spostamenti nel piano orizzontale.
Tutti questi spostamenti sono dovuti alle sollecitazioni meccaniche che l'intera arma subisce durante lo sparo e più precisamente durante la prima fase del rinculo, ovvero quella che si verifica mentre il proiettile percorre la canna.
La pressione assiale contro il piano di culatta, quella contro la spalla del bossolo, la forza scambiata tra proiettile e canna e, infine, le vibrazioni che l'accompagnano, provocano un movimento istantaneo tipo "colpo di frusta".
E' da rilevare che la prima fase del rinculo è caratterizzata dalle massime pressioni all'interno dell'arma e dalle massime deformazioni elastiche del materiale.
Si verificano, quindi, le massime accelerazioni, alle quali però, corrispondono spostamenti relativamente piccoli. In realtà l'effetto di rinculo che ognuno può macroscopicamente osservare si verifica dopo che il proiettile ha abbandonato l'arma, cioè quando essa "restituisce" al tiratore l'energia immagazzinata. Nella prima fase del rinculo l'arma non ruota attorno al punto di appoggio (la spalla del tiratore, nel caso del fucile) ma attorno al suo baricentro.
Ai fini balistici, l'effetto pratico è una variazione, negativa o positiva, dell'angolo di tiro. Questa variazione è strettamente dipendente dal tipo di arma, dal sistema di costruzione delle canne, dalla loro forma, dal materiale usato, dal sistema di incassatura, dalla carica impiegata e da fattori contingenti (ad esempio un diverso stato di umidità dell'aria può indurre movimenti nel legno dell'incassatura che viene a poggiare diversamente contro la canna ed a modificarne le vibrazioni).
In linea di massima, l'angolo di rilevamento è negativo in alcune artiglierie, ma è sempre positivo nelle armi portatili.
Nelle armi di grosso calibro può raggiungere il valore di un grado, mentre nei fucili è dell'ordine di alcuni minuti di grado. In caso di traiettorie brevi e tese l'angolo di rilevamento può quindi superare di più volte l'angolo di tiro. Così, ad esempio, in un fucile semiautomatico cal.7,9 mm. (Vo = 755 ms.) puntato sui 100 m. , l'angolo di tiro è di 3' e l'angolo di rilevamento è pari a 12'.
Può così verificarsi in casi particolari il fenomeno apparentemente strano secondo cui, diminuendo la velocità del proiettile, questo colpisce più in alto e non più in basso, come ci sarebbe da attendersi. Ciò deriva dal fatto che varia il tempo di percorrenza della canna e quindi il proiettile più lento la abbandona nel momento in cui la sua rotazione (impennamento) ha acquistato una maggiore ampiezza.
Questo fenomeno può comportare notevoli variazioni nella precisione tra un'arma azzerata al banco e la stessa arma impiegata dalla spalla oppure con canna appoggiata malamente a supporti che ne modificano le vibrazioni.
Il cacciatore o il tiratore, comunque, non devono preoccuparsi dell'angolo di rilevamento poiché di esso si è tenuto conto nell'azzerare l'arma.
Se invece si debbono eseguire calcoli con armi di altro tipo o per lunghe gittate, trascurare il rilevamento, può comportare un errore significativo.
La misura dell'angolo di rilevamento non è molto semplice in quanto occorrerebbe, con arma fissata al banco, stabilire su di un bersaglio posto ad alcuni metri, il punto esatto in cui il prolungamento dell'asse della canna incontra il bersaglio e poi, sparando un colpo, osservare quanto questo dista, in altezza, dal punto precedente.
La difficoltà di stabilire il punto in cui l'asse della canna incontra il bersaglio, può essere aggirata ricorrendo al calcolo.
Il procedimento da seguire è il seguente.

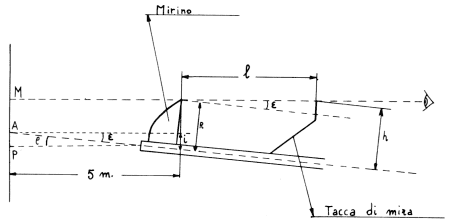
Mirando con la tacca di mira e il mirino si spari contro un bersaglio verticale posto ad esempio a 5 metri; il centro del foro prodotto dal proiettile sia P; si misuri accuratamente la distanza k della sommità del mirino dall'asse della canna e l'analoga distanza h della tacca di mira nonché la distanza l (elle) tra i due punti di mira e sia, ad esempio: h = 27,5 mm,   k = 25 mm,   l= 600 mm

Il valore dell'angolo e sarà dato da

Da cui e = 0° 14' 19"
Il valore di "i", a sua volta, sarà dato da
i = tang e * 5000 = 20,8 mm
MA = (k - i) = 4,2 mm

La distanza cercata tra i punti A e P è quindi di 4,2 mm e perciò l'angolo di rilevamento sarà dato da
tang r = 4,2/5000; r = 0° 2' 53"

  Si ricorda che per correggere il tiro bisogna operare sul mirino oppure sulla tacca di mira; se il proiettile finisce a destra del centro del bersaglio occorre o spostare il mirino verso destra oppure spostare la tacca di mira verso sinistra (e se necesario combinare i due spostamenti)

La torsione dell'arma
La torsione di un'arma, la sua inclinazione cioè verso un lato o l'altro, così che la linea di mira non si trovi nello stesso piano verticale dell'asse della canna, è causa di un errore di tiro.
Per comprendere il fenomeno si esamini la figura in cui è rappresentato il caso limite dell'arma adagiata su di un fianco, con uno spostamento di 90' rispetto alla posizione normale (si pensi ad una pistola appoggiata su di un tavolo, invece che impugnata).

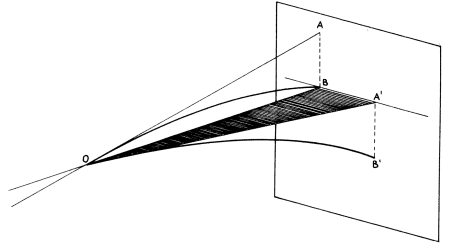
La linea di mira è calcolata in modo da compensare la caduta del proiettile alla distanza di azzeramento e quindi l'arma, in posizione normale e mirando il bersaglio B,spara in effetti in direzione di A; se l'arma viene adagiata sul fianco destro, la canna verrà a trovarsi diretta verso A con uno spostamento verso destra AB=BA'.
Nel procedere verso il punto A' il proiettile subirà l'influenza della attrazione terrestre e, in definitiva, colpirà il punto B' in cui AB=A'B'.
Si può quindi concludere che la torsione dell'arma verso destra o verso sinistra comporta uno spostamento del proiettile dal medesimo lato della torsione nonché uno spostamento verso il basso e che la torsione comporta una diminuzione della gittata in funzione diretta dell'angolo di torsione.
Sulla base di considerazioni abbastanza semplici si dimostra che quanto più la traiettoria è tesa, tanto minore è l'errore cagionato dalla torsione per cui, posto quale indice della radenza di una traiettoria
R = X/yv
lo spostamento laterale del proiettile, per angoli di torsione non troppo grandi, sarà dato da
BA' = 2X*sen2y/R
e lo spostamento verticale da
A'B' = 4X ( cosy - 1)/R
in cui y indica l'angolo di torsione.
Esempio:
Sia da calcolarsi l'influenza della torsione di un fucile pari a 15°, in relazione al proiettile già esaminato 7x64 e sia quindi Vo = 850 ms;  X = 300 m;  T = 0,411" ; yv = 0,17 m;  R = 1764

Lo spostamento in altezza può quindi ritenersi trascurabile, mentre lo spostamento laterale è indubbiamente rilevante.
Nella pratica venatoria è normale che l'arma subisca una torsione di alcuni gradi senza che il cacciatore possa accorgersene, ma fino a 5 gradi l'errore è trascurabile (nell'esempio, uno spostamento di circa 5 cm.). Sparando da posizioni anormali può accadere facilmente che la torsione sia maggiore e quindi tale da influenzare l'esito del tiro. E' appena il caso di dire che in gare di tiro una torsione anche modesta, può compromettere seriamente il risultato.
L'accorciamento della traiettoria per effetto della torsione è dato dalla formula
X(cosy -1)
E la diminuzione del tempo di volo dalla formula
T(cosy - 1)
Ad esempio nel caso appena visto si avrebbe
Diminuzione di X = 300 (cos15°-1) = - 10,2 m
Diminuzione di T = 0,41 (cos 15° - 1) = - 0,014"
Vediamo comunque di semplificare ulteriormente le cose, visto che non sono rilevanti i millimetri.
In linea generale vale la regola che
torsione a sinistra = colpo basso a sinistra
torsione a destra = colpo basso a destra
In via semplificata, posto F quale spazio di caduta del proiettile nel tempo di volo sino al bersaglio si avrà
BA' = F sen y
A'B' = F cos y
Il calcolo dimostra che nel tiro venatorio fino a 100 metri la torsione fino a 5° (che è quella che può ancora sfuggire al cacciatore non attneto) è trascurabile. L'errore per la torsione aumenta con più l'arma è azzerata per lunghe distanze. Nei calcoli fatti si è sempre considerato che l'arma fosse azzerata sul bersaglio. Un proiettile lento ssubisce la torsione più di uno veloce.
La seguente tabella contiene alcuni esempi pratici.

Palla	Angolo	100 m				200 m			300 m
		BA'		A'B'		BA'		A'B'	BA'	A'B'
6,5x54 M. Sch. 10,3 gr Vo=670 ms DOA 140 m	1°	0,2	0		1		0		1,7	0
	5°	1,1	0		5		0,2		13,1	0,6
	10°	2,2	0,2		10		0,9		26	2,3
7 x 64 10,5 gr Vo=880 ms DOA 175 m	1°	0,1	0		0,6		0		1,5	0
	5°	0,6	0		2,8		0,1		7,3	0,3
	10°	1,3	0,1		5,7		0,5		14,5	1,3
7 Rem. Mag 9,4 gr Vo=1005 ms DOA 210 m	1°	0,1	0		0,4		0		1,0	0
	5°	0,5	0		2,1		0,1		5,2	0,2
	10°	0,9	0,1		4,2		0,4		10,3	0,9

email - Edoardo Mori	top

Sitemap: in Italiano | auf Deutsch | in English |

http://www.earmi.it - Enciclopedia delle armi © 1997 - 2003