
 |
| back |
Per impostare il problema, ricordiamo come viene svolta la prova di resistenza di una barra di acciaio. Useremo, per quanto possibile, simboli e definizioni unificate UNI.
Nella apposita macchina viene inserita una barra cilindrica di prova di lunghezza L0 e di sezione S0. Essa viene poi sottoposta ad una trazione continua fino alla rottura; la barra subisce un allungamento e una diminuzione della sezione. Chiameremo L la lunghezza sotto carico e d il diametro sotto carico. DL = L - L0 è la deformazione longitudinale totale; e = DL / L0 = (L-L0) / L0 è la deformazione longitudinale unitaria. La macchina registra la forza di trazione F e l'allungamento ΔL. Si rapporta F alla sezione iniziale S0 e si indica con σ = F / S0 la tensione normale o carico unitario.
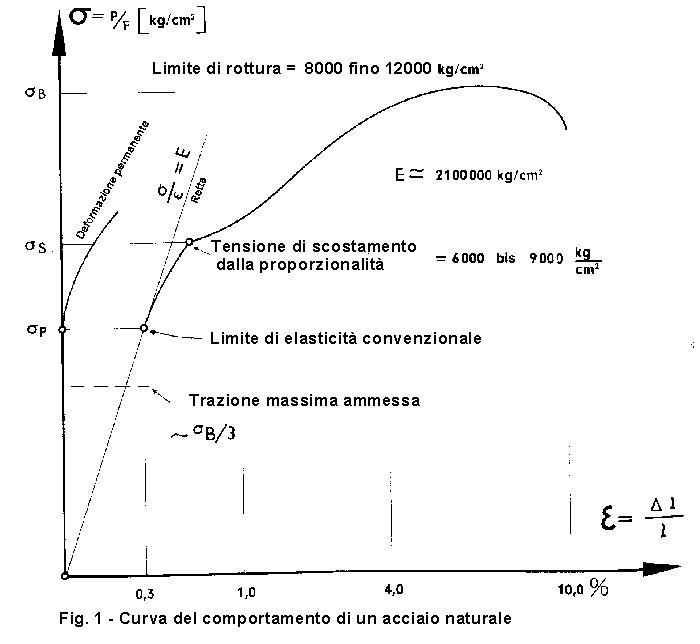
Per valori di carico crescenti, il diagramma tensioni - deformazioni è dato dalla fig. 1, nella quale e è rappresentata in percento della lunghezza iniziale del tratto di barra campione considerato. La curva di trazione così ottenuta varia a seconda dei materiali.
Vi si osserva che, per un certo tratto iniziale, sino a sp (limite di elasticità convenzionale), le deformazioni sono proporzionali alle tensioni con legge lineare e, al cessare della sollecitazione, la barra reagisce elasticamente e ritorna alle dimensioni iniziali. Per il valore assoluto della deformazione permanente si suole adottare per gli acciai lo 0,002% e per gli altri materiali (leghe leggere) lo 0,01%. Superata la tensione di proporzionalità, le deformazioni cessano di essere proporzionali ai carichi e la retta si trasforma in una curva, fino a ss (tensione di scostamento dalla proporzionalità). Dopo questo punto, il materiale comincia il processo di snervamento con deformazioni che aumentano disordinatamente anche in regime di minori tensioni, per poi regolarizzarsi con deformazioni plastiche che seguono una curva abbastanza regolare.
Nelle armi verranno usati acciai con elevato limite di rottura ottenuto con apposte leghe o con incrudimento per martellatura, oppure con la tempera.
Per la valutazione degli acciai che ci riguardano ha importanza solo il tratto di curva della figura 1 fino al punto limite di elasticità, cioè rientranti nella legge di Hooke (deformazioni proporzionali ai carichi secondo un modulo di elasticità E = s / e).
Acciai naturali e talvolta acciai temprati seguono un percorso rettilineo fino ad un pronunziato limite di elasticità σs.
È chiaro che nelle armi non si dovrà mai raggiungere il limite della deformazione permanente e che, anzi, vi dovrà essere un buon margine di sicurezza.
Non deve essere neppure trascurato il comportamento dell'acciaio per effetto del calore. In acciai naturali la resistenza cala a partire dal 350° ed a 600° è solo il 65% di quella iniziale. Con il raffreddamento si recupera la resistenza iniziale. Gli altri due tipi di acciaio invece, sottoposti alla temperatura di 350° per un certo lasso di tempo, non recuperano più la resistenza iniziale.
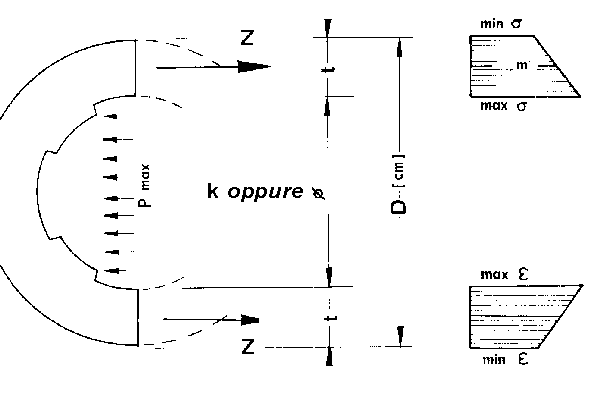
Per rinvenire le formule circa la massima resistenza delle canne di armi, partiamo dalla figura 2, nella quale è schematizzata una sezione di canna con:
D = diametro esterno
d = diametro interno
t = spessore di canna.
Pmax = la massima pressione interna
s = la tensione indotta nel materiale; supporremo inizialmente che il carico unitario s sia uguale in ogni punto della sezione di canna, come se si trattasse di un campione sottoposto a trazione assiale. Quindi, ci riferiremo ad un
sm medio.
Z = la forza di trazione esercitata sulla canna.
Per semplificare, consideriamo che la pressione interna raggiunge il suo massimo valore operando su mezza sezione di canna, che deve resistere per non essere spezzata secondo una direttrice. E’ la cosiddetta formula delle caldaie, impiegata per calcolare lo spessore dei recipienti cilindrici in pressione e, ripetiamo, si tratta di un’approssimazione.
La fisica ci dice che la condizione di equilibrio si ottiene quanto la somma delle sollecitazioni unitarie è bilanciata dalla somma delle reazioni elastiche del materiale. Cioè : ΣH = 0. Nel caso in esame avremo:
Pmax . d = 2 Z
Dalle formule 2 e 3 ( in cui il cerchietto barrato o crociato indica il diametro interno) si ricava
![]()
che inserito nell'equazione (1) ci dà (5)
![]()
da cui (6)
![]()
dove k è il diametro interno.
Questa "formula delle caldaie" ci fornisce un trazione unitaria media, mentre a noi interessa la sollecitazione massima sopportabile dall'acciaio delle nostre armi. Sul lato destro della figura 2 vediamo il vero andamento della tensione ricercata, cioè il suo andamento rispetto alla deformazione.
Dalla linea dello allungamento-deformazione di figura 1 vediamo che noi dobbiamo limitarci a lavorare nell'ambito delle deformazioni elastiche inizialmente descritte da un tratto rettilineo della curva in cui, secondo la legge di Hook, sarà (7)
E = σ/ε
Se scriviamo (8) σ = E ·ε, si vede che con un modulo di elasticità
E = 2.000.000 - 2.200.000 kp/cm²,
la tensione è direttamente proporzionale alla deformazione.Ed ancora dal diagramma delle tensioni possiamo prevedere (fig. 2) che (9)
![]()
da cui (10)
![]()
Ed infine l'affermazione decisiva:
La canna allargatasi internamente ed esternamente per effetto della pressione
dei gas, non ha cambiato il suo peso e il suo volume e quindi si può dire che per un determinato tratto s la sua superficie netta è rimasta immutata (11)
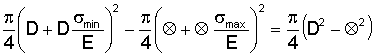
Il valore di π/4 può essere eliminato.
Siccome dalla formula 10 si ha che (13)
![]()
dalla combinazione delle formule (11) e (13) si ha la (14) 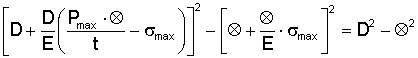
Abbiamo perciò ottenuta un'espressione in cui l'unica incognita è σmax.
L'espressione rimane comunque ancora un po' complicata; essa può essere semplificata calcolando un valore ausiliario γ per il rapporto D/Ø e per E= 2.100.000 kp/cm².
Il valore di γ può essere calcolato con l'espressione (14a) 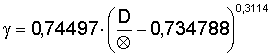
Le formule così semplificate diventano perciò (15)
![]() (16)
(16) ![]()
Controlliamo questa formula partendo dalla formula (10)
Dalla formula (15) si ricava che la formula (6) per le caldaie è un'ipotesi speciale della formula (15) quando D/Ø = 1; perciò sarà γ> = 0,5 e σmax = σmin = σm.
Il rapporto γ/0,5 ci dice quante volte σmax è maggiore di σm secondo (17) ![]()
Il nostro esempio nr. 3 ci mostrerà che la deformazione percentuale sull'interno della canna, deve essere più grande di quella sul lato esterno in modo che rimanga inalterata la superficie della sezione.
Ai fabbricanti di canne di armi è nota la formula di Lamé in cui, posto D/Ø = a, si ha (16)
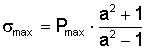
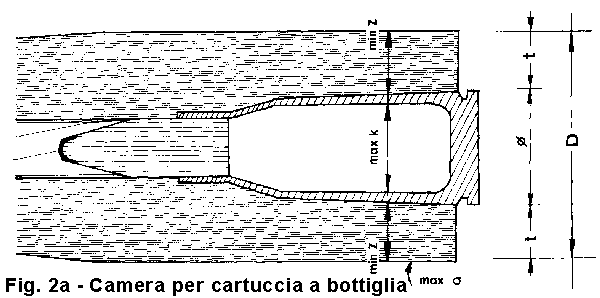
Se ora proviamo a fare un esempio pratico vedremo che la formula serve per ottenere un risultato approssimato. Essa non ci consente di valutare adeguatamente la resistenza del bossolo nella camera di cartuccia.. Nella figura 2a si vede quale è il punto critico di una canna di carabina che invece può essere agevolmente calcolato con la formula (15), usando i simboli indicati in figura.
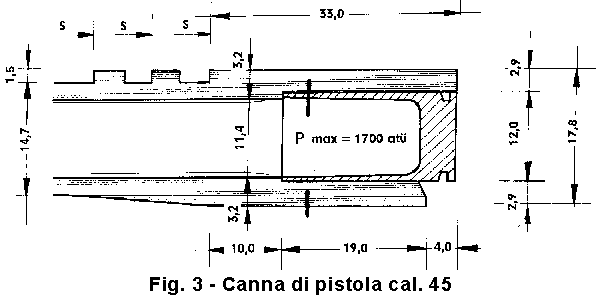
Esempio I
Dalla figura 3 possiamo acquisire i dati principali; la sezione X mostra chiaramente che si tratta della sezione soggetta alle maggiori sollecitazioni. Sia ora la pressione massima di una munizione usuale di 1700 at; nella prova forzata della canna, con una sovrapressione del 30%, si arriverà a 2200 at. Secondo la formula (14a) avremo
![]()
e dalla (15)
![]()
Dalla (16) avremo
![]()
La cartuccia di prova con una pressione di 2200 at dà, secondo la (15),
![]()
Perciò l'acciaio da usare per la nostra arma dovrebbe avere all'incirca le seguenti caratteristiche:
Limite di elasticità di almeno 7.000 kg/cm² (o 70 kg/mm²)
Limite di allungamento di almeno 8.000 kg/cm² (o 80 kg/mm²)
Limite di rottura di almeno 12.000 kg/cm² (o 120 kg/mm²)
Con questo acciaio, denominato appunto 80/120, avremo perciò i seguenti margini di sicurezza
Elasticità 7000/5960 = 1,17
allungamento 8000/5960 = 1,34
Rottura 12000/5960 = 2,02
Dopo la prova forzata non rimane alcuna deformazione permanente.
Ci sarebbe ancora da aggiungere che nella figura 3 sulla canna si trovano due camme per la chiusura dell'otturatore. queste tre zone di pressione sollecitano ulteriormente la canna. Nell'esempio 2 vedremo come tenerne conto.
Esempio 2
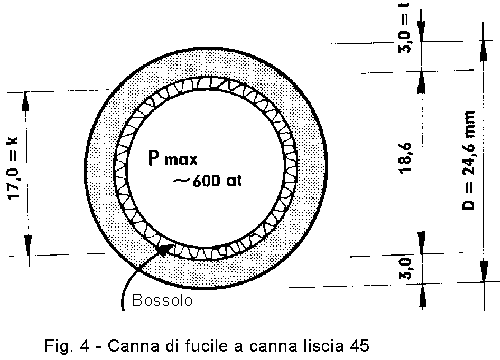
Ricaviamo i dati dalla figura 4
Dalla formula (14a) si ha che
![]()
Dalla (15)
![]()
e dalla (16)
![]()
La cartuccia di prova con una pressione di 800 at ci dà, in base alla (15)
![]()
Siccome l'otturatore ha una chiusura rigida, le camme produrranno anche una forza traente longitudinale della grandezza (19) ![]()
Questa forza si distribuisce sulla superficie sezionale della canna (20) e (21)
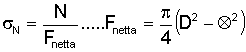
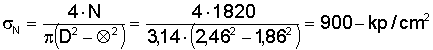
Abbiamo quindi due diverse tensioni, σmax e σN da cui bisogna derivare una tensione σg lungo un solo asse. Omettendo alcuni passaggi troppo complicati si perviene alla formula (22)
![]()
Questa formula trova adeguata corrispondenza con i dati dell'esperienza in caso di sollecitazioni statiche. Inoltre non essendo ancora ben chiariti i fenomeni correlati al rapidissimo aumento della pressione, conviene usare la formula ridotta (23)
![]()
L'impiego della formula (23) nel nostro esempio ci dà la tensione massima con le munizioni di prova
![]()
Circa le caratteristiche dell'acciaio da usare, vale quanto detto all'esempio 1. Con un acciaio 60/90 avremo, ad esempio un valore di 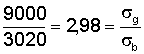
Applicando la formula per caldaie (6) alla pressione di 800 at avremmo
![]()
con un valore minore, per le ragioni viste.
Esempio 3
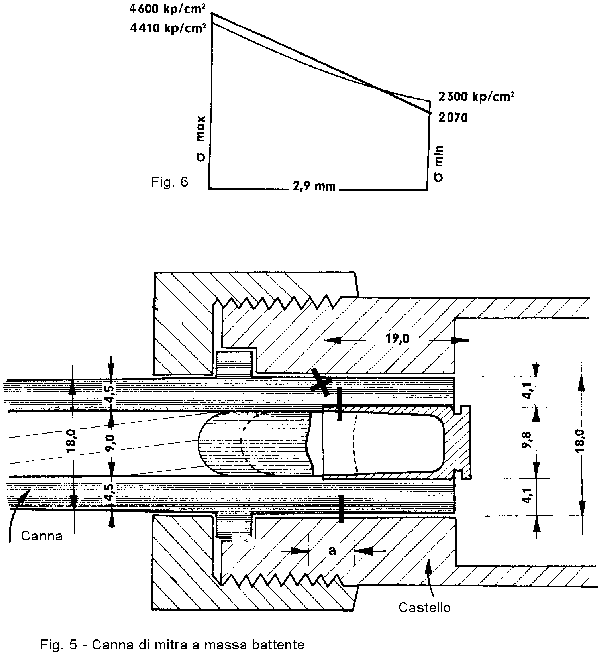
Nella figura 5 è raffigurata la sezione di un mitra; dalla figura ricaviamo la sezione X da calcolare e gli altri dati. Il proiettile si è mosso in avanti di 4-6 mm e si trova nella posizione in cui si verifica la massima pressione (posizione che dipende da moltissima fattori). La cartuccia standard produrrà una pressione massima di 2500 at e la cartuccia di prova 3250 at. La canna di 20 cm, rastremata, ha un peso di 220 gr. Supponiamo che l'attrito medio del proiettile sia di 150 kg e la cadenza di fuoco 10 colpi al secondo (caricatore di 30 colpi).
In base alla formula di Lamé (18) si ha
![]()
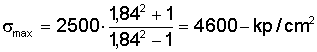
Il valore di gamma per D/Ø = 1,84 è pari a 0,77. Perciò la cartuccia normale, secondo le formule (15) e (16) ci dà ![]()
mentre σmin sarà eguale a 1260 kp/cm².
La cartuccia di prova forzata, sostituendo nelle stesse formule il valore di 3250 a 2500, ci darà σmax = 5500 kp/cm².
Facciamo la prova con la formula (10) e avremo ![]()
Usando l'acciaio di cui al primo esempio, 80/120, 7000/8000/12.000 kp/cm².
Con la cartuccia standard (in parentesi quelli per la c. di prova) avremo valori di sicurezza pari a
7000/4220 = 1,66 (1,27)
8000/4220 = 1,89 (1,45)
12000/4220 = 2,84 (2,18)
Se inseriamo i valori trovati nella formula (12) possiamo calcolare l'entità della deformazione interna ed esterna alla pressione di 2500 at.
Diametro esterno
![]()
Diametro interno
![]()
![]()
Va detto infine che sono stati sviluppati altri metodi di calcolo, ciascuno dei quali porta a risultati diversi, così che l'elaborazione matematica deve essere presa solo come una indicazione molto approssimativa.
Nota: Testo tratto da un articolo di K.H. Velte, DWJ 1967,952. Revisione di L. Golino
| Sitemap: in Italiano | auf Deutsch | in English | |
| http://www.earmi.it - Enciclopedia delle armi © 1997 - 2003 |