Frammenti di bombe o proiettili

Il problema della proiezione di frammenti  ad opera di una esplosione concerne sia i frammenti dell’involucro contenente l’esplosivo (bomba, proiettile, ordigno) sia i frammenti della struttura demolita dall’esplosione.
Le variabili sono troppe perché si possa costruire un modello matematico  preciso e si possono dare solo indicazioni di massima per valutazioni orientative. Ogni dato di qesto scritto va usato con molto spirito critico, tenendo sempre presente che la mia compertnzna in materia è limitata!
Gli effetti sono molto variabili anche in relazione alla massa dell’esplosivo.
L’esplosione provoca un’onda d’urto con un elevato picco iniziale che  si esaurisce in pochi millisecondi; poi la pressione cala lentamente. Come l'onda passa, la pressione oscilla una o più volte tra fasi positive e negative. Quando la pressione è al di sopra di quella ambientale, l'onda d'urto si dice in fase positiva. La condizione opposta è chiamata la fase negativa. A causa della differenza di pressione all'interno dell'onda d'urto, l'aria viene portata da alta a bassa pressione. Questo crea un vento di esplosione, che può essere di notevole velocità, oltre 160 kmh. La velocità di propagazione è costante (velocità del suono). La pressione riflessa può essere da 2 ad 8 volte quella diretta.
L’onda d’urto è caratterizzata da un fronte di pressione che quando incontra un ostacolo in parte lo attraversa e in parte viene riflessa con un’onda pulsante.

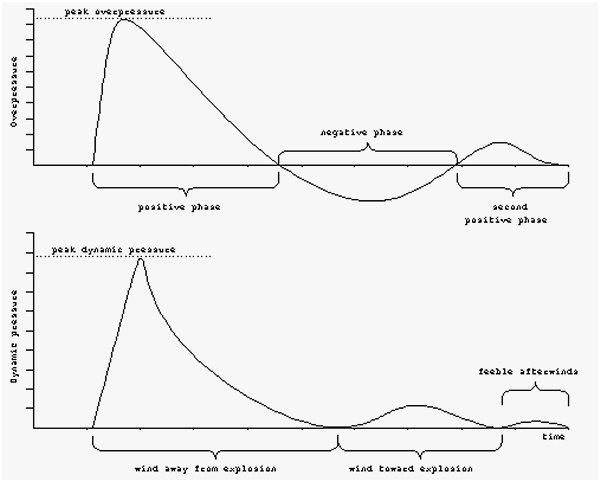
Onda di pressione
L'argmento è stato ampiamente trattato nella pagina generale sugli  esplosivi a cu si rinvia. Ecco una tabella delle pressioni in bar calcolate per 5 kg di TNT-equivalenti  alle varie distanze

Per una bomba a mano di 160 gr di TNT-eq si ottiene 320 psi =22  kg/cmq iniziali.
La formula vale per una esplosione libera; se l’esplosivo è a contatto con il suolo il picco di pressione in orizzontale può arrivare a dimezzarsi.
È stato calcolato il livello di pericolosità della sovrapressione sul corpo umano:
1,5 kg/cmq   : lesioni minime
2,5 kg/cmq  : lesioni modeste
3 kg/cmq     : lesioni gravi
10 kg/cmq   : lesioni mortali
Una protezione con indumento balistico diminuisce il rischio del 25% .
Questi dati sono intesi per grandi masse di esplosivo, oltre il quintale; infatti a  parità di pressione, la lesività decresce se diminuisce il quantitativo di esplosivo in quanto diminuisce il tempo di azione del picco di pressione.
Ecco il grafico che indica il picco di sovrapressione e la pressione dinamica in funzione della distanza dall’origine dell’esplosione di un kg di TNT.

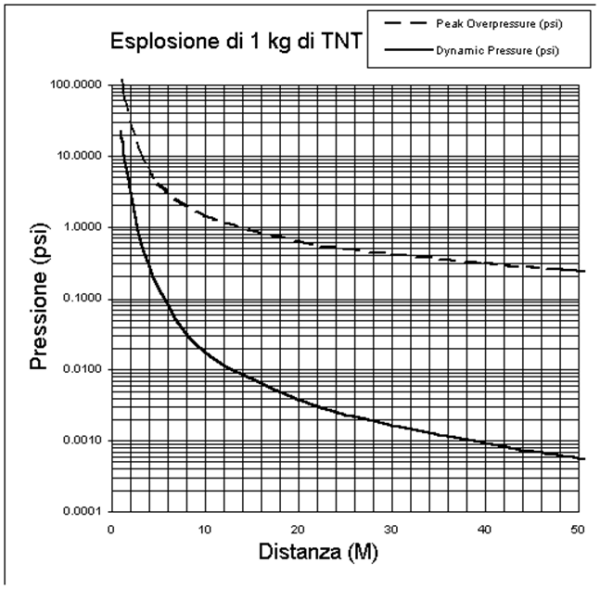
E questi sono i danni prevedibili alle strutture :

Ricordo che :
1 psi = 6'894,76 Pa = 6,894 kPa = 0,069 bar = 0,703 mH2O = 51,715 mmHg = 0,689 N/cm² = 0,068 atm = 0,0703 kg/cm² = 144 lbf/ft² = 2,31 ftH2O.
1 km/cm2 = 14,22 psi

L’esplosione di un ordigno o di una bomba o di un proiettile provoca la proiezioni di frammenti di varie dimensioni.  Una grossa bomba d’aereo  si frammenta in oltre 2000 pezzi il 50% dei quali va da 1,5 a 10 grammi di peso. Frammenti di artiglieria con peso di 0,3 - 0,5 gr. producono ferite penetranti, anche nel torace, fratturano ossa facciali e tibia se hanno una energia cinetica di 100-120 J/cmq . Penetrano nel muscolo per 6-8 cm.
La forma dei frammenti  (salvo i casi di involucri preintagliati) è estremamente variabile  con bordi frastagliati, come se il materiale fosse stato strappato; quindi sono molto taglienti. Essi raggiungono velocità di 1000-1500 m/s ma, a causa dell’elevata resistenza che oppongono all’aria e quando hanno un peso inferiore a mezzo grammo, non sono più letali dopo 5 metri di volo.
È quasi impossibile individuare un modello matematico della balistica dei frammenti, men che  approssimativo.
Esiste una formula (formula  di Gurney)  che consente di calcolare approssimativamente la velocità iniziale di un frammento
Dati:
C – La massa della carica esplosiva
M – La massa dell’involucro
V – Velocità iniziale dei frammenti
 - La Costante di Gurney relativa all’esplosivo usato e che indica il calore di esplosione in J/kg. Essa viene espressa in unità di velocità (ad es. millimetri per microsecondo o chilometri per kg). In via molto approssimativa essa è pari a 1/3 della velocità di detonazione.
 Ecco i valori della costante per alcuni esplosivi:

Se la carica ha forma di cilindro, come in bombe o proiettili esplosivi , la formula da usare  è

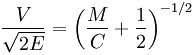
Se la carica è sferica

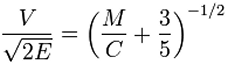
La velocità massima inziale che sia assume raggiungibile da un frammento è di 4600 m/s

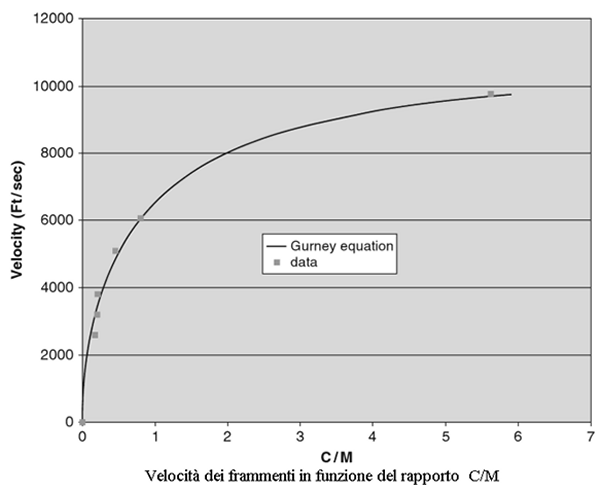
Esempio: trovare la velocità iniziale di frammenti di una bomba a mano M-61
La M-61 utilizza 185 g di Comp-B (costante di Gurney = 2770 m/s)  e l’involucro  pesa 210 g.  Il rapporto fra carica e metallo è
M/C = 210/185  = 1,135
Utilizzando il fattore per oggetti di forma sferica  K = 3 / 5 si ha
 v o = 2100 m/s ; in realtà i frammenti di una bomba a mano non superano i 1500 m/s   e sono innocui dopo 250 metri circa.
Ecco i dati sperimentali per i frammenti di  una bomba a mano russa:

La seguente tabella sperimentale per un proiettile da 105-mm M1 dà una indicazione realistica sul comportamento dei frammenti. La distanza massima raggiunta dal frammento più pesante e più veloce è  590 m. Il raggio di rischio è di circa 100 metri, ma con un calo drastico di probabilità  di colpire un avversario oltre i 25 m. dal punto di impatto. La bomba è considerata sicuramente letale entro i 5 m. In genere nei proiettili il rapporto esplosivo involucro è di 0,1 – 0,2.

Un’altra formula  consente di valutare la perdita di velocità del frammento dopo un certo percorso è la seguente:

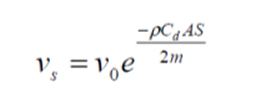
In cui  ρ è la densità dell’aria (1,2 Kg/mc)
Cd è il coeff. aerodinamico
A  l’area sezionale del frammento
S la distanza in metri
M il peso del frammento in kg
Sia ad esempio da trovare la velocità a 100 metri dalla scoppio di un frammento di M61. Se:
Vo= 2100 m/s
A= 1 cmq
Cd = 0,5
m = 2g
ρ = 1,2

si avrà

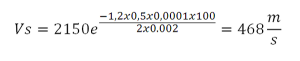
A 6 m  Vs sarebbe di 1920 m/s, a 10 metri  1800 ms; a 20 m  1555.
Il problema è ovviamente di stabilire il coeff. aerodinamico da impiegare; 0,5, come suggerito nell’esempio sopra riportato, è il cx per un proiettile ideale che viaggia a 6 Mach, con variazione possibile fra 0,4 e 0,6; ma un frammento rotante  presenta una resistenza infinitamente maggiore (anche 7 volte). Se si assimila il frammento ad un dato si ha un cx di 0,8 per velocità subsoniche e di 1,5 - per velocità ultrasoniche, con buoni risultati:

Il calcolo può comunque essere fatto con qualunque programma di balistica /ad es. Winballit) utilizzando un coefficiente aerodinamico pari ad 1,5 se si assume un comportamento del frammento simile a quello di una sfera e pari a 2  se si assume che esso opponga la stessa resistenza all’aria di un cilindro.
Questo appare essere il coefficiente più realistico considerando che il frammento viaggia con un movimento rotatorio vorticoso e con una forma e superficie continuamente variabili. Quando la velocità del frammento scende sotto la velocità del suono il cx va ssunto pari a 0,8 - 1.
In pratica il frammento oppone, istantaneamente, al flusso d'aria relativo, un'area (superficie proiettata) durante il volo a causa del tumbling o della rotazione. In prima approssimazione il frammento può essere concepito come collocato con diversi orientamenti nel flusso d'aria, in un intervallo temporale discreto, nel quale si possa definire un particolare numero di Mach uguale in tutto l'intervallo temporale di riferimento. Se si mediassero nell'intervallo tempo considerato, tutte le variabili fluidodinamiche associate allora potremmo utilizzare un coefficiente aerodinamico pari ad 1,5 (comportamento del frammento simile a quello di una sfera) o pari a 2  (comportamento del frammento simile a quello di un cilindro): quest'ultimo appare essere il coefficiente più realistico considerando che il frammento (assimilabile ad un parallelepipedo) viaggia con un movimento rotatorio vorticoso proiettando sempre una differente superficie nel flusso d'aria relativo. Quando la velocità del frammento scende sotto la velocità del suono il Cx andrebbe assunto, nelle ipotesi di partenza, pari a 0,8 - 1. Ma i coefficienti che ho indicato sopra a naso, corrispondono abbastanza agli studi teorici.

Per il brillamento di proiettili, per il caso in cui sia non possibile una proiezione tale da non consentire di raggiungere la massima gittata, si consiglia una distanza di sicurezza, assolutamente sovrabbondante, data dalla formula: 
D = 370* Peso/kg^1/5, nel caso di un solo proiettile e di
D = 650*Peso/kg^1/5, nel caso di proiettili accatastati.

Per altre informazioni si veda la pagina sugli Esplosivi .